Назад | Содержание | Вперед
Как известно из курса линейной алгебры, с помощью умножения вектора на матрицу можно выполнить различные линейные преобразования. Это и перенос, и поворот вокруг оси, и масштабирование. Основное достоинство матриц это то, что несколько последовательных преобразований в заданном порядке можно представить одной единственной матрицей.
Во всех дальнейших примерах будем полагать, что вектор у нас представлен строкой с четырьмя компонентами, а матрица, соответственно, имеет размеры 4 на 4.
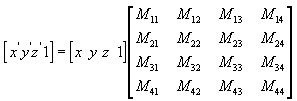
В виде уравнений
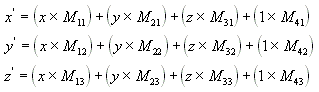
Для переноса точки используется следующее преобразование
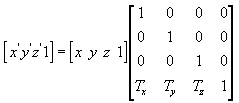
Для масштабирования (вытягивания/сжатия в направлении осей координат)
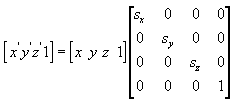
Для вращения вокруг оси X
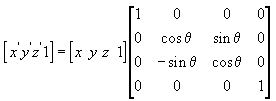
Для вращения вокруг оси Y
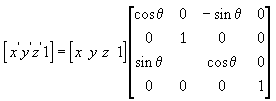
Для вращения вокруг оси Z
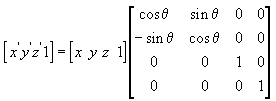
В программе эти матрицы получаются непосредственной инициализацией.
Умножение матрицы на матрицу и вектора на матрицу также не представляют ничего сложного. Главное помнить правило умножения: элемент результирующей матрицы берется как сумма произведений соответствующих компонент строки левой матрицы на компоненты столбца правой матрицы (естественно необходимо равенство размерности строк левой матрицы и столбцов правой).
Во время преобразования иногда необходимо знать как меняются вектора без учета переноса. Например необходимо повернуть треугольник вместе со своей нормалью. В этом случае вектор умножается на матрицу как обычно, но нижняя строка матрицы берется нулевой.
Для целей трассировки иногда полезно знать обратную матрицу. Простейший способ её найти через миноры и определитель. Напомним, что минор элемента матрицы есть определитель матрицы, полученной после вычеркивания строки и столбца, содержащих данный элемент. Элемент обратной же получается как отношение минора транспонированной матрицы к определителю исходной матрицы, взятое со знаком минус, если сумма номера строки и столбца элемента является нечетной. Например так:
void ReverseMatrix(Matrix *res, const Matrix &m)
{
REAL d = m.Determinant(), k;
if (d == 0)
throw "Matrix invalid";
k = 1/d;
for (int i = 0; i < 4; i++)
for (int j = 0; j < 4; j++)
if ((i + j)%2 == 0)
res->m[j][i] = m.Minor(i, j)*k;
else
res->m[j][i] = - m.Minor(i, j)*k;
}
REAL Matrix::Minor(int i, int j) const
{
REAL a[3][3];
int i0, j0, i1, j1;
for (i1 = 0, i0 = 0; i1 < 3; i1++, i0++)
{
if (i0 == i)
i0++;
for (j1 = 0, j0 = 0; j1 < 3; j1++, j0++)
{
if (j0 == j)
j0++;
a[i1][j1] = m[i0][j0];
}
}
return
+ a[0][0]*a[1][1]*a[2][2] + a[0][1]*a[1][2]*a[2][0] + a[0][2]*a[1][0]*a[2][1]
- a[0][2]*a[1][1]*a[2][0] - a[0][0]*a[1][2]*a[2][1] - a[0][1]*a[1][0]*a[2][2];
}
REAL Matrix::Determinant() const
{
return
+ _00*_11*_22*_33 - _00*_11*_23*_32 - _00*_12*_21*_33 + _00*_12*_23*_31
+ _00*_13*_21*_32 - _00*_13*_22*_31 - _01*_10*_22*_33 + _01*_10*_23*_32
+ _01*_12*_20*_33 - _01*_12*_23*_30 - _01*_13*_20*_32 + _01*_13*_22*_30
+ _02*_10*_21*_33 - _02*_10*_23*_31 - _02*_11*_20*_33 + _02*_11*_23*_30
+ _02*_13*_20*_31 - _02*_13*_21*_30 - _03*_10*_21*_32 + _03*_10*_22*_31
+ _03*_11*_20*_32 - _03*_11*_22*_30 - _03*_12*_20*_31 + _03*_12*_21*_30;
}
Процедура выполняется примерно 2000 тактов. После развертка циклов нахождения миноров (без i и j) все занимает около 700 тактов (можно увидеть в исходных кодах трассировщика).
Назад | Содержание | Вперед