Динамические программы

На главную
Программы
Статические | Полезные

Динамические программы

Игра Жизнь

Эту игру придумал математик ДЖ. Конуэй.

Все происходит на бесконечном клетчатом поле. В каждой клетке может находится организм. Развитие поколения происходит дискретно под действием определенных "генетических законов". Конуэй тщательно подбирал свои правила "на практике", добиваясь, чтобы они по возможности удовлетворяли трем условиям:

Не должно быть ни одной исходной конфигурации, для которой существовало бы простое доказательство возможности неограниченного роста популяции.
В то же время должны существовать такие начальные конфигурации, которые заведомо обладают способностью беспредельно развиваться.
Должны существовать простые начальные конфигурации, которые в течение значительного промежутка времени растут, претерпевают разнообразные изменения и заканчивают свою эволюцию одним из следующий трех способов: полностью исчезают (либо из-за перенаселенности, то есть слишком большой плотности фишек, либо наоборот, из-за разреженности фишек, образующих конфигурацию); переходят в устойчивую конфигурацию и перестают изменяться вообще или же, наконец, выходят на колебательный режим, то есть бесконечный цикл превращений с определенным периодом.

Короче говоря, правила должны быть такими, чтобы поведение популяции было непредсказуемым.

Каждая клетка имеет 8 соседей.

Правила игры сводятся к следующему:

ВЫЖИВАНИЕ. Каждая живая клетка, имеющая две или три соседние живые клетки, выживает и переходит в следующее поколение.
ГИБЕЛЬ. Каждая живая клетка, у которой больше трех соседей, погибает, из-за перенаселенности. Каждая живая клетка, вокруг которой свободны все соседние клетки или же занята всего одна клетка, погибает от одиночества.
РОЖДЕНИЕ. Если число живых клеток, с которыми граничит какая-нибудь пустая клетка, в точности равно трем (не больше и не меньше), то на этой клетке происходит рождение нового "организма".

Гибель и рождение всех "организмов" происходит одно временно. Вместе взятые, они образуют одно поколение или, как можно выразится, один "ход" в эволюции начальной конфигурации.

Популяция непрестанно претерпевает необычные, нередко очень красивые и всегда неожиданные изменения.

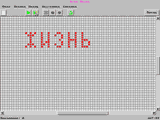
Программа позволяет играть на поле 200*200. Можно выбирать интересные готовые конфигурации и изменять правила. На последнем снимке изображено, во что превращается слово "ЖИЗНЬ" в 196 поколении.

Скачать (67 Кб)

Молекула метана

Со второго семестра нас стали считать уже взрослыми и задания мы стали выбирать уже сами. Я написал модель молекулы метана. Молекулу можно вращать, изменять размеры атомов и расстояние между ними. Также можно вращать источник света и изменять интенсивность освещения.

Скачать (29 Кб)

Многогранники

В одно время с молекулой метана была написана и эта программа. Нужно было изобразить пересечение многогранника плоскостью. К сожалению, исходный код я случайно удалил и не смог доработать программу – удалить невидимые ребра.

Скачать (70 Кб)

Редактор значков

Летом 2002 года я написал свою первую серьезную программу. Она занимала около 2000 строчек. Для меня это тогда было очень много! К тому же, ничего про формат ICO-файлов я не знал и экспериментально разбирался в их устройстве.

Это было после 10 класса, и тогда Сергей Залманович еще не научил меня хорошему стилю оформления программ (потому что я еще не успел поучиться в университете). Я сейчас даже представить не могу, как можно было так писать: после запятых никогда не было пробелов, и не объявлялись никакие константы. Правда, отступы тогда я уже делал, иначе просто не смог бы такую программу написать. До сих пор помню, как мучился с кнопками и всем остальным. Ведь каждая координата каждой кнопки упоминается в программе не один раз. Для того, чтобы подобрать хорошее положение кнопки нужно было изменять числа во всех этих местах! С гораздо меньшими трудностями я писал игру Жизнь на втором курсе.

Например, с помощью этой программы я нарисовал такой значок для Turbo Pascal.

К сожалению, исходник когда-то потерялся. Я даже не понимаю, как сохранилась сама программа. Ей можно пользоваться с помощью клавиатуры, совершенно обходясь без мыши. В программе даже есть несколько секретов. Один действует, если одновременно нажать Ctrl+Alt+Shift и обе кнопки мыши. Было еще что-то, но я уже не помню.

Скачать (28 Кб)

Доска Гальтона

На первом курсе у меня было задание изобразить доску Гальтона с движущимися по ней (одновременно несколькими) шариками. При встрече препятствия шарик с равной вероятностью продолжает путь направо или налево. Распределение шариков по ячейкам должно подчиняться определенному закону.

Скачать (40 Кб)

Поверхности

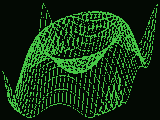На лекциях по программированию на первом курсе в качестве примера использования графики в Turbo Pascal мы писали (в тетрадях) программу, которая строит поверхности для функции двух переменных. На одной лекции мы вывели все формулы, но программу написать не успели. Дома я попробовал написать ее самостоятельно. Было очень интересно потом сравнивать, что некоторые вещи я написал точно так же, как Сергей Залманович, и подмечать то, что он реализовал лучше.

В функции я добавил параметр (время), и получилась динамическая поверхность. Очень интересно смотреть, как она вся колышется и изгибается.

Скачать (60 Кб)

Шарики

По экрану летают шарики и сталкиваются друг с другом. Получается Броуновское движение. Можно задать один большой шарик и много маленьких и смотреть, как все вокруг суетсятся, а большой шарик перемещается спокойно и неспешно.

Скачать (46 Кб)