Вычисление определенных интегралов

 

Постановка задачи:

Приближенно вычислить интеграл .

Идея:

Разобьем отрезок интегрирования [a, b] на n равных частей и пусть . Очевидно, что, чем больше мы будем брать n, тем точнее будет вычисляться интеграл. После разбиения получится последовательность точек:
.
Теперь рассмотрим формулы, которые основанны на разбиении отрезка на n частей.

Формула трапеций

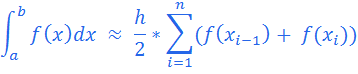
Для того, чтобы легче понять её смысл, возьмем n = 1.
Рассмотрим теперь график некоторой фукнции:

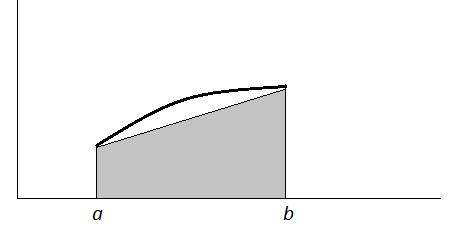
По рисунку видно, что данная формула вычисляет площадь трапеции, описанной около графика f(x), отсюда следует, что при больших n точность увеличивается.

Оценка погрешности R вычисляется по формуле:
,
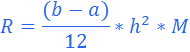где на [a, b].

Пример:
Вычислить интеграл 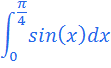, для n = 10 по формуле трапеции.

Решение.

Ответ: 0.292742644
Оценка погрешности: 0.000403728

Если судить по оценке погрешности, то первые 3 цифры в дробной части ответа верны.
Рассмотрим следующую формулу.

Формула Симпсона

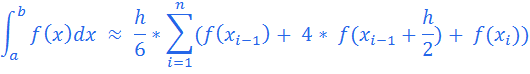
В отличие от формулы трапеции, мы пытаемся приблизить нашу f(x) многочленом 2-ой степени, т.е.
график будет описывать уже не трапеция, а парабола на каждом из отрезков разбиения, следовательно, точность будет выше, чем у формулы трапеции.

Оценка погрешности R вычисляется по формуле:
,
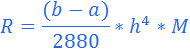где на [a, b].

Пример:
Вычислить интеграл 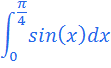, для n = 10 по формуле Симпсона

Решение.

Ответ: 0.292893223
Оценка погрешности: 0.0000000103766

Если судить по оценке погрешности, то первые 7 цифр в дробной части ответа верны.
Сравнивая результаты формулы трапеции и формулы Симпсона видно, что формула Симпсона дает более точный результат.

 

Наверх