Решение уравнений

Постановка задачи:

Пусть дано уравнение   f(x) = 0, (a, b) - интервал, на котором f(x) имеет единственный корень.
Нужно приближенно вычислить этот корень с заданной точностью.

Примечание:
Заметим, что если   f(x) имеет k корней, то нужно выделить соответственно k интервалов.

Метод половинного деления

Метод основан на той идее, что корень лежит либо на середине интервала (a, b), либо справа от середины, либо - слева, что следует из существования единственного корня на интервале (a, b).

Алгоритм:

1. Находим число ;
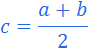2. Проверяем условие ;
3. Если оно ложно, то переходим к пункту 7;
4. Eсли   f(c)* f(a) < 0, то b = c;
5. Eсли   f(c)* f(a) > 0, то a = c;
6. Переходим к пункту 1.
7. c - искомый корень.
   

Пример:
Найти корень уравнения на интервале (0, 3) c точностью = 0.001.

Решение.

Ответ: 0.626221.

Метод простой итерации

Смысл метода простой итерации состоит в том, что мы представляем уравнение f(x) в виде и по формуле будем строить итерации, которые сходятся к искомому корню с интересующей степенью точности, но тут есть проблемы: возможно f(x) очень сложно представить в таком виде, да и не факт, что любая будет строить сходящиеся итерации, поэтому алгорим сводится к тому, чтобы оптимально найти .

Подготовка:

1. Ищем числа m и M такие, что на (a, b);
2. Представляем , где ;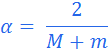

Примечание:
Такое представление является оптимальным.

Алгоритм:

1. Выбираем из (a, b);
2. Вычисляем ;
3. Проверяем условие , где ;
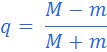4. Если оно ложно, то переходим к пункту 7;
5. ;
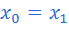6. Переходим к пункту 2;
7. - искомый корень.

Пример:
Найти корень уравнения на интервале (0, 3) c точностью = 0.001, m = 0.5, M = 3

Решение.

Ответ: 0.626271

Итог:

По результатам решения одного и того же уравнения двумя алгоритмами мы видим, что решения совпадают до четверой цифры в дробной части, что удовлетворяет заданной точности.

 

Наверх