Алгоритм Бойера-Мура

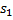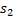Пусть даны некоторые строки и , длина которых соответственно 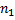и 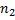. Алгоритм Бойера-Мура позволяет найти все вхождения строки 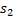в строку .

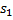Для построения таблицы сдвигов каждому символу поставим в соответствие число, которое равно минимальному количеству символов от него до конца строки (включая сам символ); всем символам, которые не содержатся в строке, ставим в соответствие 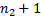, так как такие символы можно пропустить.

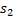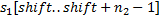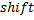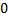В тривиальном алгоритме сравнивается с подстроками для всех от до 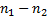. В алгоритме Бойера-Мура часть этих подстрок пропускается за счет того, что для каждого символа алфавита определен соответствующий сдвиг положения подстроки 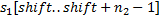. Мы будем рассматривать одну из модификаций этого алгоритма.

Реализация алгоритма построения таблицы на языке С++:

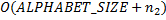std::vector<int> shifts(ALPHABET_SIZE, n2 + 1); for (int i = 0; i < n2; i++) { shifts[s2[i]] = n2 - i; }

Сложность построения таблицы равна

Рассмотрим теперь сам алгоритм:

Присваиваем 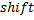значение 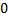. Далее будем сравнивать 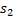с подстроками 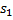посимвольно, начиная с конца, пока это возможно.
Сравниваем строк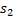и и .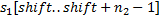
Если все символы совпали, то мы нашли вхождение .
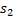Если на каком-то шаге символы не совпали, то увеличиваем 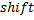на величину, которая соответствует символу .

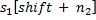Реализация алгоритма на языке С++:

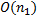int shift = 0; while (shift + n2 <= n1) { int i = n2 - 1; while (i >= 0 && s2[i] == s1[shift + i]) { i--; } if (i < 0) { return shift; } else if (shift + n2 < n1) { shift += shifts[s1[shift + n2]]; } else { break; } }

В среднем сложность алгоритма равна

, но в худшем случае можно получить

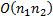. Для примера рассмотрим строк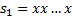и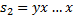

. При таких входных данных каждую итерацию внешнего цикла

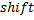будет увеличиваться всего на единицу, а внутренний цикл будет выполняться

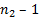раз.