
Полиномиальное хеширование
Пусть 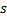 – это строка длины
– это строка длины 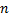 , тогда полиномиальный хеш от строки вычисляется следующим образом:
, тогда полиномиальный хеш от строки вычисляется следующим образом:
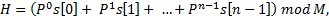
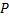 и
и 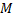 – это некоторые константы. Обычно число
– это некоторые константы. Обычно число 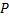 выбирается так, чтобы оно было простым и не меньшим максимального из кодов символов строки.
выбирается так, чтобы оно было простым и не меньшим максимального из кодов символов строки.Хеши обладают следующим свойством: у одинаковых строк хеши обязательно равны. Поэтому, если хеши для некоторых строк уже вычислены, то мы можем сравнить их за 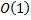 . Однако, с некоторой вероятностью мы получим неверный результат, т.е. произойдет коллизия. Поэтому с помощью полиномиального хеширования решаются те задачи, в которых вероятность коллизий мала, иначе при совпадении хешей строки нужно дополнительно проверять на равенство.
. Однако, с некоторой вероятностью мы получим неверный результат, т.е. произойдет коллизия. Поэтому с помощью полиномиального хеширования решаются те задачи, в которых вероятность коллизий мала, иначе при совпадении хешей строки нужно дополнительно проверять на равенство.
Алгоритм Рабина-Карпа
В качестве примера применения полиномиального хеширования рассмотрим задачу поиска подстроки в строке. Пусть нам требуется найти все вхождения строки 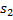 длины
длины 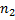 в строку
в строку 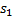 длины
длины 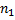 . Будем считать, что
. Будем считать, что 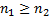 .
.
Вычислим сначала хеши для всех префиксов строки 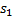 и запишем их в массив
и запишем их в массив 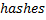 . То есть
. То есть 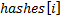 – это хеш для подстроки
– это хеш для подстроки 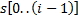 . Тогда мы можем за
. Тогда мы можем за 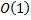 вычислить хеш
вычислить хеш 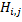 , домноженный на
, домноженный на 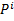 , любой подстроки
, любой подстроки 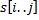 из формулы
из формулы
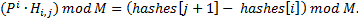
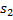 . Осталось пройти по всем подстрокам
. Осталось пройти по всем подстрокам 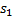 длины
длины 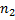 , вычисляя их хеши и сравнивая с хешем
, вычисляя их хеши и сравнивая с хешем 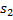 .
.Реализация алгоритма на языке С++:
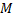 опускается, то есть вычисления производятся по модулю
опускается, то есть вычисления производятся по модулю 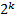 , где
, где 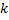 зависит от используемого типа. Сложность алгоритма равна
зависит от используемого типа. Сложность алгоритма равна 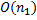 .
.| |
Житов Александр, 2018 ФПМКТиФ ВоГУ |