Префикс-функция

Рассмотрим строку 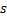. Будем обозначать 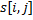подстроку строки 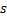, которая начинается с 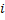-го символа и заканчивается символом с индексом 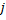. Префикс-функцию от строки 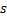определим с помощью массива, который будем обозначать 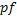. 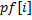– это длина наибольшего префикса подстроки 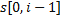, совпадающего с ее суффиксом (но не равного самой подстроке ).

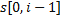Алгоритм вычисления

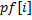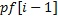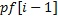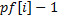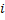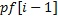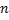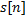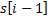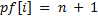Заметим сначала, что превосходит не более чем на единицу, т.к. в противном случае в качестве значения мы бы должны были взять число . Рассмотрим шаг алгоритма с номером . Мы уже знаем значение , обозначим его за . Eсли совпадает с , то , и можно переходить к следующему шагу алгоритма:

.

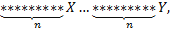
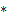где – символ строки, 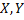– символы которые нужно сравнить (префикс и суффикс могут «накладываться» друг на друга). Если же 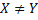, то нужно рассмотреть префикс длины 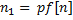. Предположим, что это не так, то есть, что существует префикс подстроки 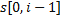длины 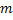, такой что 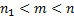и совпадающий с суффиксом длины :

.

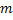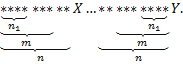
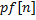Это невозможно, т.к. в качестве значения мы должны были бы взять 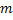. Аналогично, если длина 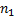не подходит, то проверять нужно 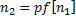, и т.д.

Реализация алгоритма на языке C++:

На каждом шаге внешнего цикла значение префикс-функции увеличивается не более чем на единицу, поэтому 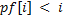. На каждом шаге внутреннего цикла значение 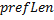уменьшается не менее, чем на единицу. Отсюда следует, что суммарное количество итераций внутреннего цикла ограничено числом итераций внешнего. Таким образом, сложность алгоритма можно оценить как .

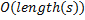Задача о количестве различных подстрок

Приведем пример задачи, которая решается с помощью префикс-функции. Пусть 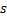– это некоторая строка. Требуется найти количество ее различных подстрок.

Будем решать задачу с помощью динамического программирования. На каждом шаге алгоритма будем добавлять в строку по символу из 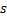и искать количество получившихся новых подстрок. Рассмотрим шаг алгоритма с номером 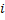. Пусть 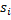– текущая строка, то есть 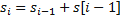. Нам нужно найти количество новых подстрок, которые заканчиваются символом 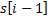. Для этого «перевернем» строку 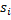и обозначим ее 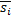. Таким образом, задача сводится к поиску суффиксов подстрок 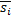, совпадающих с ее префиксом, который теперь начинается с нового символа 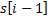. Заметим, что достаточно найти только максимальный такой суффикс, т.к. все меньшие суффиксы будут в нем содержаться. Соответственно, количество новых подстрок, полученных на данном шаге, можно будет найти по формуле

.

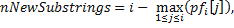
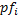где – это префикс-функция, вычисленная для 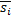. Пусть 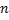– это длина строки 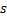. Тогда мы 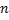раз будем добавлять по символу и каждый раз заново вычислять префикс-функцию. Значит сложность алгоритма составит .

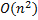Реализация решения задачи на языке C++: