Суффиксный массив

Пусть 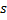– это некоторая строка длины 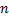. Подстроку, которая начинается с 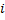-го символа и заканчивается символом с индексом 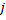, будем обозначать 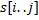. Суффиксный массив для строки 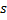– это массив, состоящий из суффиксов 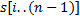, отсортированных в лексикографическом порядке. Каждому суффиксу можно поставить в соответствие индекс его первого символа, поэтому в массиве достаточно хранить числа от 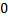до .

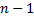Рассмотрим пример. Пусть дана строка 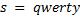, тогда список отсортированных суффиксов, пронумерованных с нуля, для нее будет выглядеть так:

2. erty

0. qwerty

3. rty

4. ty

1. werty

5. y

То есть суффиксный массив для строки

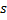имеет вид

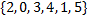Алгоритм построения

Сортировку суффиксов строки сведем к сортировке циклических сдвигов строки 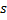вида 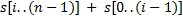. Для этого добавим в конец строки некоторый символ, который будет меньше остальных символов строки. Далее подстрокой будем считать циклическую подстроку, то есть подстроку 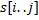, которая при 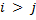равна строке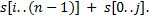

Сортировка происходит следующим образом: поэтапно сортируются подстроки длины 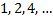, пока их длина не станет больше длины исходной строки. На каждом шаге, кроме первого, сравнение строк происходит на основании данных, полученных на предыдущем шаге.

Для построения нам понадобятся два вспомогательных массива. Обозначим их 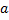и 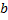. Подстроки 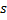могут быть равны. На каждом шаге будем разбивать сортируемые подстроки на группы равных, причем номера группам будем присваивать в соответствии с лексикографическим порядком следования подстрок. Информация об этом будет храниться в массиве 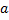. В массиве 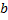будем хранить индексы первых символов подстрок. Эти индексы также будут идти в соответствии с лексикографическим порядком.

Рассмотрим шаг алгоритма с номером 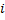. Нам уже известны массивы 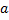и 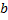для предыдущего шага. Заметим, что любую подстроку длины 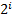при 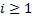можно разбить на две подстроки длины 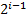. А строки такой длины мы сравнивали на предыдущем шаге и информация об этом хранится в массиве 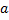. Пусть, например, требуется сравнить подстрок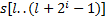и и 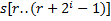. Сравним сначала подстрок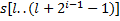и и 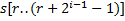, то есть проверим равенство 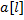и 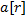. Пусть 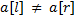, тогда первая строка меньше второй, если 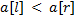. Если же 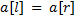, то аналогично нужно сравнить 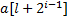и . 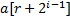Таким образом, мы можем построить новый массив 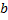за 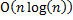, так как сравнение подстрок выполняется за 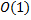. Далее по нему можно найти новые значения массива 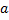. Всего будет примерно 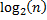шагов, поэтому общая сложность составляет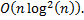

Реализация алгоритма на языке С++:

std::vector<int> b(n); for (int i = 0; i < n; i++) { b[i] = i; } std::sort(b.begin(), b.end(), [&] (int l, int r) { return s[l] < s[r]; }); std::vector<int> a(n); a[b[0]] = 0; int curClassNumber = 0; for (int i = 1; i < n; i++) { if (s[b[i]] != s[b[i - 1]]) { curClassNumber++; } a[b[i]] = curClassNumber; } int curLength = 1; while (true) { std::sort(b.begin(), b.end(), [&] (int l, int r) { if (a[l] != a[r]) return a[l] < a[r]; else return a[(l + curLength) % n] < a[(r + curLength) % n]; }); std::vector<int> newA(n); newA[b[0]] = 0; curClassNumber = 0; for (int i = 1; i < n; i++) { if (a[b[i]] != a[b[i - 1]] || a[(b[i] + curLength) % n] != a[(b[i - 1] + curLength) % n]) { curClassNumber++; } newA[b[i]] = curClassNumber; } std::swap(a, newA); if (curLength == n) break; curLength = std::min(curLength * 2, n); }

Задача о поиске подстроки

Приведем пример задачи, которая решается с помощью суффиксного массива. Пусть 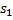и 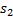– это некоторые строки длины 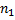и 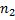соответственно. Требуется найти вхождения 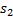в 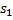. Заметим, что 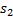, если она входит в 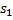, является префиксом некоторого суффикса строки 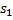. Пусть мы имеем суффиксный массив для 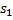. Тогда 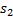можно искать с помощью двоичного поиска. Для проверки является ли строка 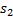префиксом нужно провести не более 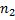сравнений. Таким образом, если мы имеем уже вычисленный суффиксный массив, то сложность поиска произвольной строки 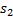равна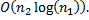

Заметим, что все суффиксы, для которых 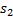совпадает с их префиксом, будут идти подряд в суффиксном массиве. Следовательно, если требуется найти все вхождения 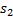в 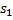, то достаточно выполнить двоичный поиск дважды.