Растровая развёртка эллипса

Выполнил студент третьего курса

отделения прикладной математики

Шнуровский Виктор

 

Данный алгоритм является модификацией алгоритма генерации окружности, предложенного Джеком Брезенхемом

Уравнение эллипса имеет вид . Перепишем его следующим образом: b²x²+a²y²=a²b²

Рассмотрим точку с абсциссой x_m=. Касательная к эллипсу в этой точке будет составлять угол 45º. Тогда эллипс в первой четверти можно построить в два этапа: сперва при изменении абсциссы от 0 до x_m, затем от a до x_m.

Алгоритм Брезенхема пошагово генерирует очередные точки эллипса, выбирая на каждом шаге для занесения пикселя точку растра P_i(x_i,  y_i), ближайшую к истинному эллипсу, так чтобы ошибка ε(P_i) = b²x_i²+a²y_i² - a²b² была минимальной.

Рассмотрим генерацию части эллипса, лежащей в первой четверти, по часовой стрелке при изменении абсциссы от 0 до x_m.

Проанализируем возможные варианты занесения i-й точки, после занесения i–1 -й.

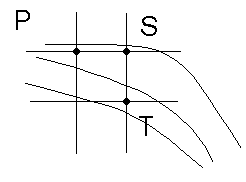
При генерации эллипса в рассматриваемой области после занесения точки P(x_i-1, y_i-1) следующая точка может быть (см. рис) либо S (x_i-1+1, y_i-1) - перемещение по горизонтали, либо T (x_i-1 + 1, y_i-1 - 1) - перемещение по диагонали. Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра эллипса до точки и эллипса:

|S_i| = |(x_i-1+1)² b² + y_i-1²a² – a²b²|

|T_i| = |(x_i-1+1)² b² + (y_i-1 - 1)²a² – a²b²|

Выбирается и заноситься та точка, для которой это значение минимально. Для определения того, какой пиксель выбрать, составим разность

d_i = |S_i| - |T_i|= |(x_i-1+1)² b² + y_i-1²a² – a²b²| - |(x_i-1+1)² b² + (y_i-1 - 1)²a² – a²b²|

И будем выбирать T_i если d_i > 0 и S_i если d_i ≤ 0.

Попробуем избавиться от модулей. Возможны 3 случая:

1.     S_i > 0, а T_i < 0. Тогда d_i = S_i + T_i.

2.     S_i > 0, а T_i > 0. Тогда надо будет выбрать точку T_i. Если рассмотрим d_i = S_i + T_i, то оно, очевидно, будет положительным, что соответствует точке T_i

3.     S_i < 0, а T_i < 0. Тогда надо будет выбрать точку S_i. Если рассмотрим d_i = S_i + T_i, то оно, очевидно, будет отрицательным, что соответствует точке S_i

Одним словом, знак выражения d_i = S_i + T_i определяет следующую точку однозначно. Преобразуем его следующим образом:

d_i = S_i + T_i = 2(x_i-1+1)² b² + 2y_i-1²a² +  a² - 2y_i-1 a² - 2a²b² =

= 2x_i-1²b² + 4x_i-1b² + 2b² + 2y_i-1²a² + a² - 2y_i-1 a² - 2a²b² (*)

Выведем рекуррентную формулу для d_i. Для этого рассмотрим разность d_i+1 - d_i.

d_i+1 - d_i = 2x_i²b² + 4x_ib² + 2b² + 2y_i²a² + a² - 2y_i a² - 2a²b² – (2x_i-1²b² + 4x_i-1b² + 2b² +

2y_i-1²a² + a² - 2y_i-1 a² - 2a²b²)

Так как x_i = x_i-1 + 1, то d_i+1 - d_i = 4b²x_i-1 + 6b² + 2a²(y_i - y_i-1) (y_i + y_i-1+1)

Если на i-ом шаге выбрана точка S, то y_i = y_i-1 и d_i+1= d_i + 4b²x_i-1 + 6b²; а если точка P, то y_i = y_i-1 – 1 и d_i+1= d_i + 4b²x_i-1 + 6b² - 4 a² y_i-1

Подставляя в формулу (*) начальные значения x = 0 и у = b, получаем, что d₁ = 2b² +  a² - 2b a²

Таким образом, дуга эллипса при изменении абсциссы от 0 до x_m построена. Построение оставшейся части эллипса в первой четверти ведётся аналогично, только меняется направление просмотра и все х заменяются на у.

Эллипс целиком можно получить отображением части, лежащей в первой четверти, относительно осей координат и начала координат. Это делает процедура Pixel4.

 

procedure Pixel4(xc, yc, x, y : integer);

begin

  PutPixel(xc + x, yc + y, cc);

  PutPixel(xc + x, yc - y, cc);

  PutPixel(xc - x, yc + y, cc);

  PutPixel(xc - x, yc - y, cc)

end;

 

procedure Ellipse(xc, yc : integer; XRadius, YRadius : Word);

var

  x, y : integer;

  xr2, yr2, d : longint;

  xm : double;

begin

  xr2 := sqr(XRadius) shl 1; yr2 := sqr(YRadius) shl 1;

  x := 0; y := YRadius; d := (yr2 - xr2 * y) + xr2 shr 1 ;

  xm := xr2 / sqrt((xr2 + yr2) shl 1) - 1;

  Pixel4(xc, yc, x, y);

  while x < xm do begin

    if d > 0 then begin

      dec(y);

      d := d + yr2 * (x shl 1 + 3) - xr2 * y shl 1    

    end

    else

      d := d + yr2 * (x shl 1 + 3);

    inc(x);

    Pixel4(xc, yc, x, y)

  end;

  d := (xr2 - yr2 * XRadius) + yr2 shr 1; x := XRadius; y := 0;

  Pixel4(xc, yc, x, y);

  xm := xm + 2;

  while x > xm do begin

    if d > 0 then begin

      dec(x);

      d := d + xr2 * (y shl 1 + 3) - yr2 * x shl 1

    end

    else

      d := d + xr2 * (y  shl 1 + 3);

    inc(y);

    Pixel4(xc, yc, x, y)

  end

end;

 

Проведённые исследования показывают, что приведённая выше процедура в 2.3 раза быстрее аналогичной из модуля Graph.