истории
криптоалгоритмам
криптосистемы
с открытым ключом
криптоалгоритмов
| Главная | |
| Немного истории | |
| Требования к криптоалгоритмам | |
| Симметричные криптосистемы | |
| Криптосистемы с открытым ключом | |
| Примеры криптоалгоритмов | |
Симметричные алгоритмы представляют собой алгоритмы, в которых ключ шифрования может бать рассчитан по ключу дешифрирования и наоборот. В большинстве симметричных систем ключи шифрования и дешифрирования одни и те же. Эти алгоритмы также называют алгоритмами с секретным ключом или алгоритмами с одним ключом. Для работы такой системы требуется, чтобы отправитель и получатель согласовали используемый ключ перед началом безопасной передачи сообщения (имели защищенный канал для передачи ключа). Безопасность симметричного алгоритма определяется ключом, т.о. раскрытие ключа дает возможность злоумышленнику шифровать и дешифрировать все сообщения.
Из-за большой избыточности естественных языков в зашифрованное сообщение трудно внести осмысленные изменения, поэтому помимо защиты информации обеспечивается защита от навязывания ложных данных. Если же естественная избыточность недостаточна, то используется специальная контрольная комбинация - имитовставка.
Так как используется один ключ, то каждый из участников обмена может зашифровывать и дешифрировать сообщения, поэтому данная схема шифрования работает на взаимном доверии. Если его нет, то могут возникать различные коллизии, так как при возникновении какого-либо спора по поводу достоверности сообщения, независимый наблюдатель не может сказать кем из участников было отправлено сообщение.
Симметричные алгоритмы делятся на две категории. Одни из них обрабатывают текст побитно(иногда побайтно) и называются потоковыми алгоритмами или потоковыми шифрами. Те же, которые работают с группами битов открытого текста называются блочными алгоритмами (шифрами).
В данном виде шифра текст пишется на горизонтально разграфленном листе бумаги фиксированной ширины, а шифротекст считывается по вертикали. Дешифрирование заключается в записи шифротекста вертикально на листе разграфленной бумаги фиксированной ширины и затем считывании открытого текста горизонтально. Открытый текст: ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
В О Л О Г О
Д С К И Й
Г О С У Д А
Р С Т В Е Н
Н Ы Й П Е
Д А Г О Г И
Ч Е С К И Й
У Н И В Е
Р С И Т Е Т
Буквы открытого текста записываются в клетки прямоугольной таблицы по ее строчкам. Буквы ключевого слова пишутся над столбцами и указывают порядок этих столбцов (по возрастанию номеров букв в алфавите). Чтобы получить зашифрованный текст, надо выписывать буквы по столбцам с учетом их нумерации:
Открытый текст: Прикладная математика Ключ: Шифр| Ш и ф р |
| 4 1 3 2 |
| П р и к л а д н а я м а т е м а т и к а |
Ключевое слово(последовательность столбцов) известно адресату, который легко сможет расшифровать сообщение.
Так как символы криптотекста те же, что и в открытом тексте, то частотный анализ покажет, что каждая буква встречается приблизительно с той же частотой, что и обычно. Это дает криптоаналитику информацию о том, что это перестановочный шифр. Применение к криптотексту второго перестановочного фильтра значительно повысит безопасность. Существуют и еще более сложные перестановочные шифры, но с применением компьютера можно раскрыть почти все из них.
Хотя многие современные алгоритмы используют перестановку, с этим связана проблема использования большого объема памяти, а также иногда требуется работа с сообщениями определенного размера. Поэтому чаще используют подстановочные шифры.
В подстановочных шифрах буквы исходного сообщения заменяются на подстановки. Замены в криптотексте расположены в том же порядке, что и в оригинале. Если использование замен постоянно на протяжение всего текста, то криптосистема называется одноалфавитной (моноалфавитной). В многоалфавитных системах использование подстановок меняется в различных частях текста.
Юлий Цезарь повествует о посылке зашифрованного сообщения Цицерону. Используемая при этом система подстановок была одноалфавитной, но не являлась системой Цезаря: латинские буквы заменялись на греческие способом, который не был ясен из рассказа Цезаря. Информация о том, что Цезарь действительно использовал систем у Цезаря, пришла от Светония.
В шифре Цезаря каждая буква замещается на букву, находящуюся k символами правее по модулю равному количеству букв в алфавите. (Согласно Светонию у Цезаря k=3 n=50)
Очевидно, что обратной подстановкой является
Обобщением системы Цезаря является аффинная криптосистема. Она определяется двум числами a и b, где 0<=a,b<=n-1. n - как и раньше, является мощностью алфавита. Числа a и n должны быть взаимно просты.
Соответствующими заменами являются:
Взаимная простота a и n необходима для биективности отображения, в противном случае возможны отображения различных символов в один и неоднозначность дешифрирования.
Система Цезаря не является старейшей. Возможно , что наиболее древней из известных является система греческого историка Полибия, умершего за 30 лет до рождения Цезаря. Его суть состоит в следующем: рассмотрим прямоугольник, часто называемый доской Полибия.
| А | Б | В | Г | Д | Е | |
| А | А | Б | В | Г | Д | Е |
| Б | Ж | З | И | Й | К | Л |
| В | М | Н | О | П | Р | С |
| Г | Т | У | Ф | Х | Ц | Ч |
| Д | Ш | Щ | Ъ | Ы | Ь | Э |
| Е | Ю | Я | . | , | - |
Каждая буква может быть представлена парой букв, указывающих строку и столбец, в которых расположена данная буква. Так представления букв В, Г, П, У будут АВ, АГ, ВГ, ГБ соответственно, а сообщение ПРИКЛАДНАЯ МАТЕМАТИКА зашифруется как ВГВДБВБДБЕАААДВБААЕБЕЕВАААГААЕВАААГАБВБДААЕЕ
В данной разновидности шифра Цезаря ключ задается числом k (0<=k<=n-1) и коротким ключевым словом или предложением. Выписывается алфавит, а под ним, начиная с k-й позиции, ключевое слово. Оставшиеся буквы записываются в алфавитном порядке после ключевого слова. В итоге мы получаем подстановку для каждой буквы. Требование, чтобы все буквы ключевого слова были различными не обязательно - можно записывать ключевое слово без повторения одинаковых букв. Количество ключей в системе Цезаря с ключевым словом равно n!.
Естественным математическим обобщением аффинных систем являются полиномиальные криптосистемы: вместо линейной функции выбирается произвольный многочлен. Но полиномиальные системы малоинтересны с точки зрения криптографии, так как главным для аффинных систем является простота управления ключом - ключ всегда состоит из последовательности 26 букв и однозначно определяется парой чисел. Представление же в виде полинома может быть слишком сложным.
Более эффективны обобщения подстановки Цезаря - шифр Хилла(Hill) и шифр Плэйфер(Playfair, в переводе "честная игра"). Они основаны на подстановке не отдельных символов, а 2-грамм (шифр Плэйфер) или n-грамм (шифр Хилла). При более высокой криптостойкости они значительно сложнее для реализации и требуют достаточно большого количества ключевой информации.
При своей простоте в реализации одноалфавитные системы легко уязвимы. Определим количество различных систем в аффинной системе. Каждый ключ полностью определен парой целых чисел a и b, задающих отображение ax+b. Для а существует j(n) возможных значений, где j(n) - функция Эйлера, возвращающая количество взаимно простых чисел с n, и n значений для b, которые могут быть использованы независимо от a, за исключением тождественного отображения (a=1 b=0), которое мы рассматривать не будем. Таким образом получается j(n)*n-1 возможных значений, что не так уж и много: при n=33 в качестве a могут быть 20 значений( 1, 2, 4, 5, 7, 8, 10, 13, 14, 16, 17, 19, 20, 23, 25, 26, 28, 29, 31, 32), тогда общее число ключей равно 20*33-1=659. Перебор такого количества ключей не составит труда при использовании компьютера. Но существуют методы упрощающие этот поиск и которые могут быть использованы при анализе более сложных шифров.
Одним из таких методов является частотный анализ. Распределение букв в криптотексте сравнивается с распределением букв в алфавите исходного сообщения. Буквы с наибольшей частотой в криптотексте заменяются на букву с наибольшей частотой из алфавита. Вероятность успешного вскрытия повышается с увеличением длины криптотекста. Существуют множество различных таблиц о распределении букв в том или ином языке, но ни одна из них не содержит окончательной информации - даже порядок букв может отличаться в различных таблицах. Распределение букв очень сильно зависит от типа теста: проза, разговорный язык, технический язык и т.п.
|
|
Хотя нет таблицы, которая может учесть все виды текстов, но есть вещи общие для всех таблиц, например, в английском языка буква E всегда возглавляет список частот, а T идет на второй позиции. A и O почти всегда третьи. Кроме того девять букв английского языка E, T, A, O, N, I, S, R, H всегда имеют частоту выше, чем любые другие. Эти девять букв заполняют примерно 70% английского текста. Ниже приведены соответствующие таблицы для различных языков.
|
|
|
|
|
|
Заметим, что буквы I, N, S, E, A (И, Н, С, Е, А) появляются в высокочастотном классе каждого языка! Также есть таблицы частоты появления букв в начале и конце слова.
Простейшая защита против атак, основанных на подсчете частот, обеспечивается в системе омофонов(HOMOPHONES) - однозвучных подстановочных шифров, в которых один символ открытого текста отображается на несколько символов шифротекста, их число пропорционально частоте появления буквы. Шифруя букву исходного сообщения, ма выбираем случайно одну из ее замен. Следовательно простой подсчет частот ничего не дает криптоаналитику. Однако доступна информация о распределении пар и троек букв в различных естественных языках. Криптоанализ, основанный на такой информации будет более успешным.
Для шифра Цезаря имеется более простой способ расшифровки - так называемый метод полосок. На каждую полоску наносятся по порядку все буквы алфавита. В криптограмме берется некоторое слово. Полоски прикладываются друг к другу так, чтобы образовать данное слово. Двигаясь вдоль полосок находится осмысленное словосочетание, которое и служит расшифровкой данного слова, одновременно находится и величина сдвига.
Полиалфавитные подстановочные шифры были изобретены Лином Баттистой (Lean Battista) в 1568 году. Основная идея многоалфавитных систем состоит в том, что на протяжении всего текста одна и та же буква может быть зашифрована по-разному. Т.е. замены для буквы выбираются из многих алфавитов в зависимости от положения в тексте. Это является хорошей защитой от простого подсчета частот, так как не существует единой маскировки для каждой буквы в криптотексте. В данных шифрах используются множественные однобуквенные ключи, каждый из которых используется для шифрования одного символа открытого текста. Первым ключом шифруется первый символ открытого текста, вторым - второй, и т.д. После использования всех ключей они повторяются циклически.
Шифр Вернама, или одноразовый блокнот, был изобретен в 1917 году Мейджором Джозефом Моборном (Major Joseph Mauborn) и Гильбертом Вернамом (Gilbert Vernam) из AT&T (American Telephone & Telegraph). В классическом понимании одноразовый блокнот является большой неповторяющейся последовательностью символов ключа, распределенных случайным образом. Первоначально это была одноразовая лента для телетайпов. Отправитель использовал каждый символ ключа для шифрования только одного символа открытого текста. Шифрование представляет собой сложение по модулю n (мощность алфавита) символа открытого текста и символа ключа из одноразового блокнота. Каждый символ ключа используется только один раз и для единственного сообщения, иначе даже если использовать блокнот размером в несколько гигабайт, при получении криптоаналитиком нескольких текстов с перекрывающимися ключами он сможет восстановить исходный текст. Он сдвинет каждую пару шифротекстов относительно друг друга и подсчитает число совпадений в каждой позиции. если шифротексты смещены правильно, соотношение совпадений резко возрастет. С этой точки зрения криптоанализ не составит труда. Если же ключ не повторяется и случаен, то криптоаналитик, перехватывает он тексты или нет, всегда имеет одинаковые знания. Случайная ключевая последовательность, сложенная с неслучайным открытым текстом, дает совершенно случайный криптотекст, и никакие вычислительные мощности не смогут это изменить.
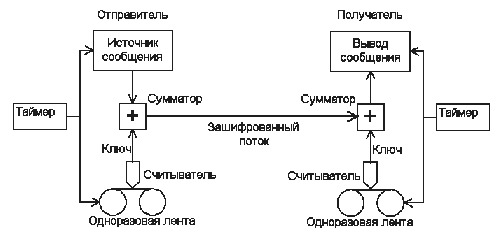В реальных системах сначала подготавливают две одинаковые ленты со случайными цифрами ключа. Одна остается у отправителя, а другая передается "неперехватываемым" образом например, курьером с охраной, законному получателю. Когда отправитель хочет передать сообщение, он сначала преобразует его в двоичную форму и помещает в устройство, которое к каждой цифре сообщения прибавляет по модулю два цифры, считанные с ключевой ленты. На принимающей стороне кодированное сообщение записывается и пропускается через машину, похожую на устройство, использованное для шифрования, которое к каждой двоичной цифре сообщения прибавляет (вычитает, так как сложение и вычитание по модулю два эквивалентны) по модулю два цифры, считанные с ключевой ленты, получая таким образом открытый текст. При этом, естественно, ключевая лента должна продвигаться абсолютно синхронно со своим дубликатом, используемым для зашифрования.
Главным недостатком данной системы является то, что для каждого бита переданной информации должен быть заранее подготовлен бит ключевой информации, причем эти биты должны быть случайными. При шифровании большого объема данных это является серьезным ограничением. Поэтому данная система используется только для передачи сообщений наивысшей секретности. По слухам "горячая линия" между США и СССР шифровалась с помощью одноразового блокнота. Многие сообщения советских шпионов были зашифрованы с использованием одноразовых блокнотов. Эти сообщения нераскрыты сегодня, и не будут раскрыты никогда (если не найдется способа вернуться в прошлое и достать эти блокноты :)
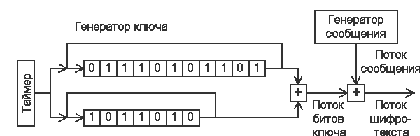Чтобы обойти проблему предварительной передачи секретного ключа большого объема, инженеры и изобретатели придумали много остроумных схем генерации очень длинных потоков псевдослучайных цифр из нескольких коротких потоков в соответствии с некоторым алгоритмом. Получателя шифрованного сообщения при этом необходимо снабдить точно таким же генератором, как и у отправителя. Но такие алгоритмы добавляющих регулярности в шифротекст, обнаружение которых может помочь аналитику дешифровать сообщение. Один из основных методов построения подобных генераторов заключается в использовании двух или более битовых лент, считанные с которых данные побитно складываются для получения "смешанного" потока. Например, простая одноразовая лента может быть заменена двумя циклическими лентами, длины которых являются простыми или взаимно простыми числами. Так как в этом случае длины лент не имеют общих множителей, полученный из них поток имеет период повторения, равный произведению их длин: две ленты, имеющие длину 1000 и 1001 соответственно, дают в результате составной поток с периодом 1000x1001=1001000 цифр. Ленты циркулируют через сумматор, который складывает по модулю два считанные с них цифры. Выход сумматора служит ключом, используемым для зашифрования сообщения. Поэтому важно, чтобы составной поток превышал по длине все вместе взятые сообщения, которые могут быть переданы за разумный период времени. Поскольку побитовый сумматор является линейным устройством, он изначально криптографически слаб, но может быть усилен большим количеством различных способов. Другой способ - указание местонахождения ключа как места в книге, например, Дональд Э. Кнут Искусство Программирования Том 2. Получисленные алгоритмы. Третье издание. стр 83, 3-й абзац. Все символы, входящие в алфавит, начиная с этого места используются как одноразовый ключ для какого-либо сообщения. Но в данном случае ключ не будет случайным и может быть использована информация о частотах распределения букв.
Как не удивительно, но класс шифров Вернама - единственный класс шифров, для которого может быть доказана (и была доказана Шенноном) невскрываемость в абсолютном смысле этого термина.
Одной из старейших и наиболее известных многоалфавитных криптосистем является система Виженера, названная в честь французского криптографа Блейза Виженера(Vigenere), в М.Н.Аршинов, Л.Е.Садовский Коды и математика данный шифр назван шифром Тритемиуса. Этот метод был впервые опубликован в 1586 году. В данном шифре ключ задается набором из d букв. Такие наборы подписываются с повторением под сообщением, а, затем, полученную последовательность складывают с открытым текстом по модулю n(мощность алфавита). Т.е. получается следующая формула:
Другой разновидностью шифра Виженера, имеющей легкозапоминаемый квадрат подстановок, является шифр Бофорта(Beaufort, в некоторой литературе читается как Бьюфорт), названный в честь адмирала сэра Френсиса Бофорта - создателя шкалы для определения скорости ветра. Его строками являются строки квадрата Виженера, записанные в обратном порядке, а первая и последняя строки поменяны местами:
| А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я | |
| А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я |
А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ч Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Ш Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Щ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ъ Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ы Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Ь Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Э Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Ю Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А Я Я Ю Э Ь Ы Ъ Щ Ш Ч Ц Х Ф У Т С Р П О Н М Л К Й И З Ж Е Д Г В Б А |
В обоих случаях обратная подстановка легко определяется из квадрата, или по формулам
Повторное применение двух или более шифров Виженера будет называться составным шифром Виженера. Он имеет уравнение
Если ключ k не повторяется, то получится шифр Вернама. Если в качестве ключа используется текст, имеющий смысл, то имеем шифр "бегущего ключа".
Такой шифр представляет собой простую подстановку с последующим применением шифра Виженера:
Дальнейшей модификацией системы Виженера является система шифров с автоключом(auto-key), приписываемая математику XVIв. Дж. Кардано, AUTOCLAVE. Шифрование начинается с помощью "первичного ключа" (который является настоящим ключом в нашем смысле) и продолжается с помощью сообщения или криптограммы, смещенной на длину первичного ключа, затем производится сложение по модулю, равному мощности алфавита. Например:
| Сообщение | П Р И В Е Т П Р И М А Т У |
| Первичный ключ | В Г П У |
| Автоключ | П Р И В Е Т П Р И |
| Шифротекст | С У Ч Х Ф В Ч Т Н Ю П В Ы |
Легальная расшифровка не представляет труда: по первичному ключу получается начало сообщения, после чего найденная часть исходного сообщения используется в качестве ключа.
В другом варианте данной системы в качестве ключа служит текст сообщения, зашифрованный с помощью ключа по системе Виженера. Но данный криптоалгоритм слабее оригинального.
Если ключ повторяется периодически и период известен, то криптоанализ данных систем может быть сведен к криптоанализу одноалфавитных систем. Пусть период равен 5. Буквы упорядочиваются по столбцам следующим образом:
| 1 | 2 | 3 | 4 | 5 |
| 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 |
| ... | ... | ... | ... | ... |
Два появления одной буквы в одном столбце представляют одну букву сообщения. Поэтому можно расшифровать каждый столбец простым подсчетом частот.
Примерно в 1860г. немецким криптоаналитиком Ф.У.Казиски(Kasisky) был изобретен метод вскрытия систем с неизвестным периодом с помощью обнаружения одинаковых слов в криптотексте. Допустим, слово ЫВАП появляется дважды с 13 буквами между двумя появлениями. Это может быть случайно, а может означать тот факт, что одинаковая часть сообщения зашифрована начиная с той же позиции ключа. Тогда расстояние между двумя Ы равно 16 и кратно длине ключа. поэтому возможная длина ключа равна 2, 4, 8, 16. Когда получается несколько таких предположений о длине ключа, некоторые из которых могут оказаться неправильными, то можно будет сделать верное предположение о длине ключа. Более длинные повторяющиеся слова предпочтительнее. Также преимуществом для криптоаналитика является повторение слов более одного раза.
Криптоанализ систем с автоключом
Криптоанализ измененной системы AUTOCLAVE проще, чем для первоначальной. Аналитику достаточно только угадать или найти длину ключа d. Тогда он может взять первую и d+1 буквы из криптотекста. Тогда, по построению, для d+1 буквы ключом является первая, следовательно из квадрата Виженера можно определить букву, стоящую на d+1 месте в открытом тексте. Подобным образом может быть раскрыт весь текст сообщения, кроме первых d букв. Первая версия данной системы, где ключом служит сдвиг исходного сообщения, неуязвима против такой простой криптоатаки.
Для раскрытия первой версии AUTOCLAVE может быть использован метод Казиски. Пусть слово ИЛИ появляется дважды в исходном сообщении и расстояние между этими появлениями равно удвоенному смещению. Тогда найдется последовательность из трех букв, например КАН, расположенная посредине между появлениями ИЛИ. Таким образом, имеется следующая часть исходного сообщения: ... ИЛИ ... КАН ... ИЛИ ...
В процессе шифрования получаем:
| Сообщение | ... ИЛИ ... КАН ... ИЛИ ... |
| Автоключ | ... ИЛИ ... КАН ... |
| Шифротекст | ... ЬЛЩ ... ЬЛЩ ... |
Таким образом, ЬЛЩ появляется дважды в криптотексте и расстояние между ними в точности равно периоду, в то время как для системы Виженера данный метод давал числа лишь кратные периоду. После того, как смещение известно, ключевое слово находится с помощью исчерпывающего поиска, основанного на подсчете частот индивидуальных букв. При получении ключевого слова все становится очевидным. Имеется n возможных набором для первой буквы ключевого слова. Когда этот выбор произведен, из него определяется первая буква сообщения, которая в свою очередь, определяет d+1, и так далее. Поэтому выбор первой буквы дает 1, d+1, 2d+1, ... буквы сообщения. Варианты, приводящие к последовательностям невозможных распределений, могут быть отброшены. Таки способом находится первая буква. Остальные d-1 букв определяются аналогично.
Режим электронной шифровальной книги (electronic codebook) - это наиболее очевидный способ использования блочного шифра: блок открытого текста заменяется блоком шифротекста. Так как один и тот же блок открытого текста заменяется одним и тем же блоком шифротекста, то теоретически возможно создать шифровальную книгу блоков открытого текста и соответствующих криптотекстов. Однако, если размер блока 64 бита, то кодовая книга будет состоять из 264 записей, что слишком много для предварительного вычисления и хранения (для каждого ключа понадобится отдельная шифровальная книга). Это самый легкий режим работы. Все блоки открытого текста шифруются независимо и, следовательно, нет необходимости в последовательном шифровании, что важно для баз данных с произвольным доступом. Кроме того, обработка может быть распараллелена, на несколько шифровальных процессоров, независимо обрабатывающих различные блоки. Проблемой данного режима является то, что если у криптоаналитика есть открытый текст и шифротекст для нескольких сообщений, то он может начать составлять шифровальную книгу, не зная ключа. В большинстве реальных ситуаций фрагменты сообщений могут повторяться. Особенно уязвимы начало и конец сообщения, где находится информация об отправителе, получателе, дате, формате файла, и т.п. Положительными чертами являются возможность шифровать несколько сообщений одним ключом без снижения безопасности и нераспространении ошибок - при повреждении неверно дешифрируется только испорченный блок.
В режиме сцепления блоков шифра перед шифрованием над открытым текстом и предыдущим блоком шифротекста выполняется операция побитового сложения (XOR). Когда блок открытого текста зашифрован, полученный шифротекст запоминается в регистре обратной связи. Прежде чем будет зашифрован следующий блок открытого текста, он подвергается операции XOR вместе с содержимым регистра обратной связи, и так далее. Таким образом, шифрование каждого блока зависит от всех предыдущих.
Дешифрирование является обратной операцией. Блок шифротекста раскрывается как обычно, но сохраняется в регистре обратной связи. Затем следующий блок дешифрируется и подвергается операции XOR вместе с содержимым регистра обратной связи, и так далее до конца сообщения.
Единственная битовая ошибка в открытом тексте влияет на данный блок шифротекста и все остальные, но при дешифрировании этот эффект инвертируется, и восстановленный открытый текст содержит ту же единственную ошибку. Битовая ошибка в блоке шифротекста влияет на открытый текст следующим образом: блок, в котором, содержится ошибка при дешифрировании испортится полностью, а в следующем блоке искажается единственный бит, находящийся в той же позиции, что и ошибочный бит. Эта ошибка не влияет на блоки, расположенные через один от испорченного, и далее, поэтому данный режим является самовосстанавливающимся - ошибка влияет на два блока, но система продолжает правильно работать для всех остальных блоков. Но если при передаче потеряется или добавится бит, то на выходе будет дешифрироваться сплошной мусор, поэтому любая криптосистема, использующая данный режим, должна обеспечивать целостность блочной структуры.