Простейшее применение псевдослучайных чисел - это метод Монте-Карло. Он появился
в 1949 году вместе с публикацией статьи Н. Метрополиса и С. Услама "Метод Монте-Карло".
Это статистический метод, который может использоваться для вычисления интегралов,
расчёта систем массового обслуживания, решения систем алгебраических уравнений.
Основная идея метода состоит в том, что моделируется случайная величина  ,
имеющая
,
имеющая 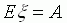 , где A - искомая величина. Для оценивания
, где A - искомая величина. Для оценивания 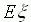 проводят
случайныю выборку из множества значений случайной величины. Хорошей оценкой
проводят
случайныю выборку из множества значений случайной величины. Хорошей оценкой 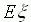 является среднее
является среднее 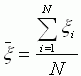 . Так как каждый конкретное значение оценки
. Так как каждый конкретное значение оценки 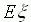 носит
случайный характер, то часто в качестве ответа указывается интервал и вероятность, с
которой точное значение
носит
случайный характер, то часто в качестве ответа указывается интервал и вероятность, с
которой точное значение 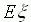 попадёт в этот интервал. Такой интервал называется доверительным.
Для более точных оценок необходимо, чтобы
попадёт в этот интервал. Такой интервал называется доверительным.
Для более точных оценок необходимо, чтобы  имела возможно меньшую дисперсию.
Теперь можно перейти к конкретным примерам.
имела возможно меньшую дисперсию.
Теперь можно перейти к конкретным примерам.
1. Задача Бюффона.
Классическая вероятностная задача, известная ещё в 18 веке. Пусть на бумаге проведены тонкие параллельные линии на расстоянии h друг от друга. На них случайным образом бросается игла длины l (l < h). Найти вероятность того что игла пересечёт одну из линий.
Решение. Рассмотрим середину иглы. Расстояние от неё до ближайшей прямой обозначим за A.
A распределена равномерно на 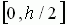 . Угол между иглой и прямой обозначим за
. Угол между иглой и прямой обозначим за 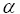 .
.
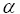 распределена равномерно на
распределена равномерно на 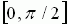 . Тогда условие пересечения иглой прямой
запишется в виде
. Тогда условие пересечения иглой прямой
запишется в виде 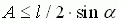 .
.
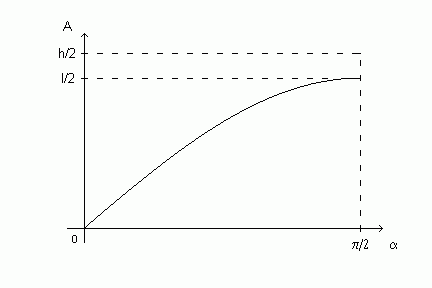
Площадь под графиком равна 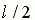 . Искомая вероятность равна
отношению площади под графиком к площади прямоугольника
. Искомая вероятность равна
отношению площади под графиком к площади прямоугольника 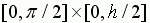 ,
, 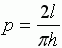 .
Так как эта вероятность оценивается экспериментально, то можно получить приближённое значение
.
Так как эта вероятность оценивается экспериментально, то можно получить приближённое значение 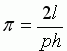 . Это
обстоятельство привело к тому, что многие математики 18-19 веков ставили такой эксперимент.
Компьютерная модель этого опыта служит лишь для демонстрации метода Монте-Карло, так как нельзя
получить случайные числа распределённые на
. Это
обстоятельство привело к тому, что многие математики 18-19 веков ставили такой эксперимент.
Компьютерная модель этого опыта служит лишь для демонстрации метода Монте-Карло, так как нельзя
получить случайные числа распределённые на 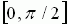 не зная
не зная 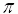 .
.
2. Вычисление определённых интегралов.
Пусть нам нужно вычислить интеграл 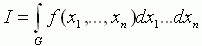 . Считая G ограниченным в
. Считая G ограниченным в 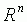 множеством, впишем его в
n-мерный параллелепипед
множеством, впишем его в
n-мерный параллелепипед 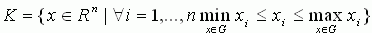 . Введём
. Введём 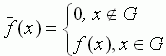 . Тогда
. Тогда 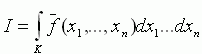 .
Очевидным представляется следующее утверждение:
.
Очевидным представляется следующее утверждение: 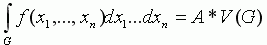 ,
где A - среднее значение f на G, а
,
где A - среднее значение f на G, а 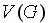 -
объём множества G.
Среднее значение
-
объём множества G.
Среднее значение 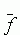 можно оценить,
промоделировав большое число m n-мерных случайных величин равномерно распределённых на множестве K.
Для этого достаточно получить m*n одномерных случайных величин, распределённых на соответствующих отрезках.
Среднее значение
можно оценить,
промоделировав большое число m n-мерных случайных величин равномерно распределённых на множестве K.
Для этого достаточно получить m*n одномерных случайных величин, распределённых на соответствующих отрезках.
Среднее значение 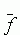 равно
равно 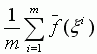 ,
где
,
где 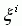 - i-я n-мерная случайная величина.
Итак
- i-я n-мерная случайная величина.
Итак 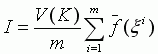 ,
, 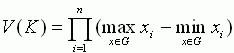 . Вычисление простых (чаще одномерных)
интегралов методом Монте-Карло не оправдано, так как квадратурные формулы работают быстрее и точнее, но
для многократных интегралов эти формулы сильно усложняются, а метод Монте-Карло почти не требует изменений.
. Вычисление простых (чаще одномерных)
интегралов методом Монте-Карло не оправдано, так как квадратурные формулы работают быстрее и точнее, но
для многократных интегралов эти формулы сильно усложняются, а метод Монте-Карло почти не требует изменений.