Очевидно, что случайные числа нельзя выработать, используя определённый алгоритм. Однако можно создать такую последовательность чисел, которая будет приближать многие свойства случайных чисел. Такие числа называются псевдослучайными. Впервые предложил их использовать Джон фон Нейман в 1946 г. Его метод состоял в следующем: n-разрядное число возводилось в квадрат и из него выбирались средние n чисел. Метод был очень несовершенен, последовательности почти всегда вырождались в 0 или зацикливались с коротким периодом. Позднее было предложено много различных алгоритмов выработки псевдослучайных чисел. Вот наиболее простые из них.

1. Линейный конгруэнтный метод.

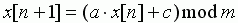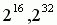Предложен Д. Х. Лемером. Основная вычислительная формула: . Алгоритм зацикливается с периодом не превышающим m. Коэффициенты a, m и x(0) могут принимать произвольные целые значения, за исключением 0. c может быть также и 0, но в этом случае сокращается период. m обычно выбирается равным и т.д., что делает ненужной операцию деления, которая автоматически выполнится при переполнении. a можно взять равным, например, 1664525, c - равным 1013904223. Такой метод часто реализуется в современных системах программирования, хотя он не применим в статистике и криптогрфии.

2. "Mother-of-All" random number generator.

Предложен Джорджем Марсальей(Marsaglia), профессором университета Флориды, США. Вычислительная формула:

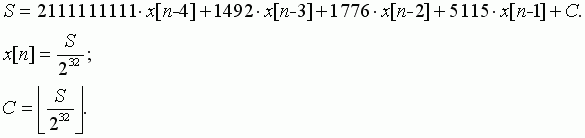
Этот алгоритм является обобщением предыдущего и избавлен от главного недостатка предыдущего метода, короткого периода. Здесь период имеет порядок 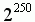. 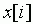принадлежат [0, 1). Начальные их значения могут быть выбраны случайно. Алгоритм может быть применён в прикладных науках, но он имеет более низкую скорость.

3. Mersenne Twister.

Предложен Макутой Матсумотой и Такеджи Нушимирой. Основная идея заключачается в том, что к начальной(инициирующей) применяется серия битовых операций. После их выполнения получается новая последовательность, первый член которой считается псевдослучайным числом. Последовательность имеет большую размерность(624 элемента), поэтому период генератора равен 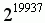. Алгоритм очень быстр из-за отсутствия умножений, но не обладает достаточной случайностью. Область применения алгоритма поэтому несколько ограничена.
Алгориму посвящён авторский сайт. Там есть реализации на разных языках, FAQ, рекомендации по использованию.

4. Генераторы типа "Xorshift".

Одни из самых новых генераторов от Джорджа Марсальи. Опять рассматривается некоторая начальная последовательность, к которой применяются операции "Xorshift". Эти операции заключаются в следующем: x[i] := x[i] xor (x[i] shl{или shr} a). Итоговое случайное число может быть получено при помощи суммирования отдельных членов последовательности, либо применения к ним операции xor. В настоящее время это один из самых используемых алгоритмов, вырабатываемая последовательность достаточно случайна, периоды - от 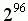(в зависимости от реализации), отсутствие умножений положительно сказывается на скорости.

5. Другие генераторы.

Можно придумать ещё много других генераторов псевдослучайных чисел, но большой интерес могут представлять комбинации уже представленных методов. В разделе программы размещён алгоритм "KISS", полученный в результате комбинации линейного конгруэнтного алгоритма, алгоритма Фибоначчи с запаздываниями и алгоритма "Xorshift". Данный алгоритм используется в игровой индустрии Северной Америки и Австралии.

Подробнее о выработке псевдослучайных чисел можно узнать в книге Д. Кнута "Искусство программирования. Том 2." и работах Джорджа Марсальи.