Случайные числа находят широкое применение в прикладных науках. Они используются в статистике, численных методах, графике, криптографии.
Нижеизложенный материал требует знания математики, читать его необязательно.
1. Определение.
Рассмотрим совокупность 
, где 
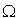- вероятностное пространство(здесь
- числовая прямая), A - 
-алгебра его подмножеств, P - вероятностная мера. Случайной
величиной называется A-измеримая функция, определённая на 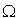. Случайные величины делятся
на дискретные и абсолютно непрерывные. Дискретные случайные величины могут быть заданы
рядом распределения с общим членом 
, где 
- случайная величина, 
- значения случайной величины, 
-
соответствующие вероятности, причём должно выполняться 
. Абсолютно непрерывные
случайные величины могут быть заданы функцией распределения 
. Функция
распределения должна быть неотрицательной, неубывающей, непрерывной слева, 
,
. Для абсолютно непрерывных случайных величин
существует плотность распределения 
.
2. Примеры случайных величин.
Биномиальное распределение.
Может интерпретироваться как некоторый эксперимент с двумя исходами. 0 - событие не наступило, 1 - событие наступило. |
Распределение Пуассона.
Достаточно хорошо описывает вероятности наступления редких событий. |
Нормальное распределение.
Функция распределения не выражается через элементарные. Нормально распределена, например, ошибка измерения некоторой величины. |
3.Числовые характеристики случайных величин.
Математическое ожидание.
|
Дисперсия и среднеквадратическое отклонение.Дисперсия |
. Интеграл
в выражении является интегралом Лебега. Математическое ожидание 
.
. Среднеквадратическое отклонение 
.
Чтобы узнать подробнее про меру, интеграл Лебега и др. смотрите ссылки.
