Сортировка Шелла

Сортировка Шелла – интересная и оригинальная модификация одной из самых (не побоюсь этого слова) банальных сортировок – сортировки вставками. Отличие в том, что гражданин Шелл, размышляя о возможности модификации сортировки вставками, решил сравнивать элементы, расположенные на некотором расстоянии друг от друга, тогда как в классической сортировке вставками сравниваются смежные элементы, поэтому окончательные позиции элементов могут устаканиваться несколько дольше, чем при сортировке Шелла.

Возникает один естественный вопрос: а какие это должны быть расстояния? Здесь начинается самое интересное. Оказывается, многое зависит от выбора этих расстояний. В частности эффективность и скорость алгоритма. Учёные мужи с момента изобретения алгоритма и до наших дней бьются над поиском лучшей последовательности шагов.

Сам Шелл делил число элементов на 2, затем полученный результат снова пополам и так далее, а результаты (без учёта остатка) деления запоминал. Получалась последовательность n/2, n/4, ..., 1 (дробной чертой здесь обозначено целочисленное деление).

Нестандартный подход к проблеме сортировки вызвал большой интерес учёных, многие из которых опытным путём установили, что последовательность Шелла не всегда оптимальна и при неудачном входном массиве сложность сортировки может достигать

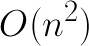
Исследователями было предложено множество различных последовательностей шагов. В частности, мне удалось найти в Интернете формулы вычисления последовательности, предложенной Седжвиком

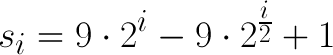
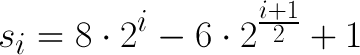
для чётных и нечётных i  соответственно.

Там же было указано, что сложность алгоритма с последовательностью Седжвика в среднем составляет около

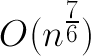
а в худшем

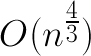
что, на мой взгляд, достаточно неплохо. Подготовимся к реализации. Для удобства напишем сортировку на Турбо Паскале, и, определив её слабые места, реализуем задуманное на ассемблере.

Const
  nmax=5000; {наибольшее число элементов массива}
Type
  data=integer; {Для определённости сортируем целые числа}
  struct=Array[0..nmax-1] Of data; {будем сортировать массив этого типа}
Procedure Sort(Var a: struct; n: integer); {процедура сортировки. По-моему,
                                не нуждается в каких-либо комментариях –
                                сортировку вставками знают все, ну а здесь
                                представлена её слегка изменённая версия :)}
  Const
    smax=32; {Наибольшее число шагов. Тридцати двух хватит с лихвой!}
  Var
    s: Array[0..smax-1] Of integer; {массив, хранящий шаги}
    i, j, k, m, n: integer;
    buf: data;
  Begin
    {Начнём с заполнения массива шагов. Пользуемся формулами Седжвика}
    i:=0;
    Repeat
      If i And 1=0 Then
        k:=9*(1 Shl i)-9*(1 Shl (i Shr 1))+1
      Else
        k:=1 Shl (i+3)-6*(1 Shl ((i+1) Shr 1))+1;
      s[i]:=k;
      i:=i+1;
    Until 3*k>n;
    {Приступаем к сортировке}
    Repeat
      i:=i-1;
      k:=s[i];
      For j:=k To n-1 Do Begin
        buf:=a[j];
        m:=j-k;
        While (m >= 0) And (buf < a[m]) Do Begin
          a[m+k]:=a[m];
          m:=m-k;
        End;
        a[m+k]:=buf;
      End;
    Until i=0;
  End;

Запускаем программу, выводим массив до того и после того, убеждаемся в работоспособности нашей реализации.

Теперь я приведу ассемблерный код своей реализации этого дела.