Сравнение алгоритмов
Скажу несколько слов о достоинствах тех или иных алгоритмов сортировки.
Итак, поразрядная. Несомненные преимущества – линейная характеристика, отсутствие сравнений и устойчивость. Всё настолько прекрасно, что кажется, будто лучше и придумать нельзя. Но радоваться рано (см. ниже).
К слову, поразрядная сортировка намного лучше приспособлена для списков, чем для массивов. В последнем случае пришлось бы в самом процессе сортировки выделять память, что по времени весьма затратно. Можно также (и это проще) создать своего рода буферный список, занести в него исходный массив, отсортировать список и перезаписать массив, но затраты памяти при таком раскладе, мягко говоря, грандиозны.
Сортировка слияниями по своей сути – достаточно интересный рекурсивный алгоритм и по сравнению с известным рекурсивным алгоритмом быстрой сортировки обладает преимуществом – устойчивостью.
Как выяснится далее, реализация этого алгоритма получилась самой быстрой из всех рассмотренных. К недостаткам метода я бы отнёс необходимость буфера под массив, однако алгоритм теоретически работает и со списками. Для списков буфер не нужен. Ещё один минус – рекурсия, для неё нужен стек.
Возможна оптимизация алгоритма. Можно ограничить глубину рекурсии, а когда массив разбивается на подмассивы достаточно малой длины, сортировать их каким-нибудь другим алгоритмом, к примеру, сортировкой вставками или даже Шелла (но тогда придётся также поэкспериментировать со значениями шагов). Для этого нужно провести отдельное исследование известных алгоритмов сортировки применительно к небольшим массивам и выбрать из них лучший по быстродействию.
Выбирая третий алгоритм для реализации, я колебался между быстрой сортировкой и сортировкой Шелла. "Быстрая сортировка... это как-то стандартно", – подумал я. А вот метод Шелла по-своему интересен, он отличается оригинальностью идеи, и пусть даже не столь эффективен для сортировки больших массивов, но предоставляет простор для исследований. Преимущество сортировки в её нерекурсивности, память под стек не требуется. Буферы также не нужны (за исключением одного-единственного регистра процессора, если речь идёт о сортировке целых 32-разрядных чисел).
Теперь хотелось бы сказать пару слов о результатах проведенного мной исследования. Стоит, однако, заметить, что оно было выполнено несколько "кустарно" (исследовалось только время, так как на практике рядовым пользователям неважно, сколько произошло сравнений, сколько пересылок и так далее) и не особо правильно – как мне кажется, не совсем верно сравнивать алгоритмы, работающие на разных структурах данных. Время сортировки измерялось API-функцией GetTickCount, а она, как известно, не обладает хорошей точностью. Тем не менее, приблизительная оценка получена.
Давайте посмотрим на графики зависимости времени сортировки от длины массива. Их я построил в программе Microsoft Excel с использованием замечательной возможности добавления линии тренда, воспользовавшись которой можно даже увидеть, уравнение какой степени у нас получилось.
Итак, первый алгоритм – поразрядная сортировка (рис. 1).
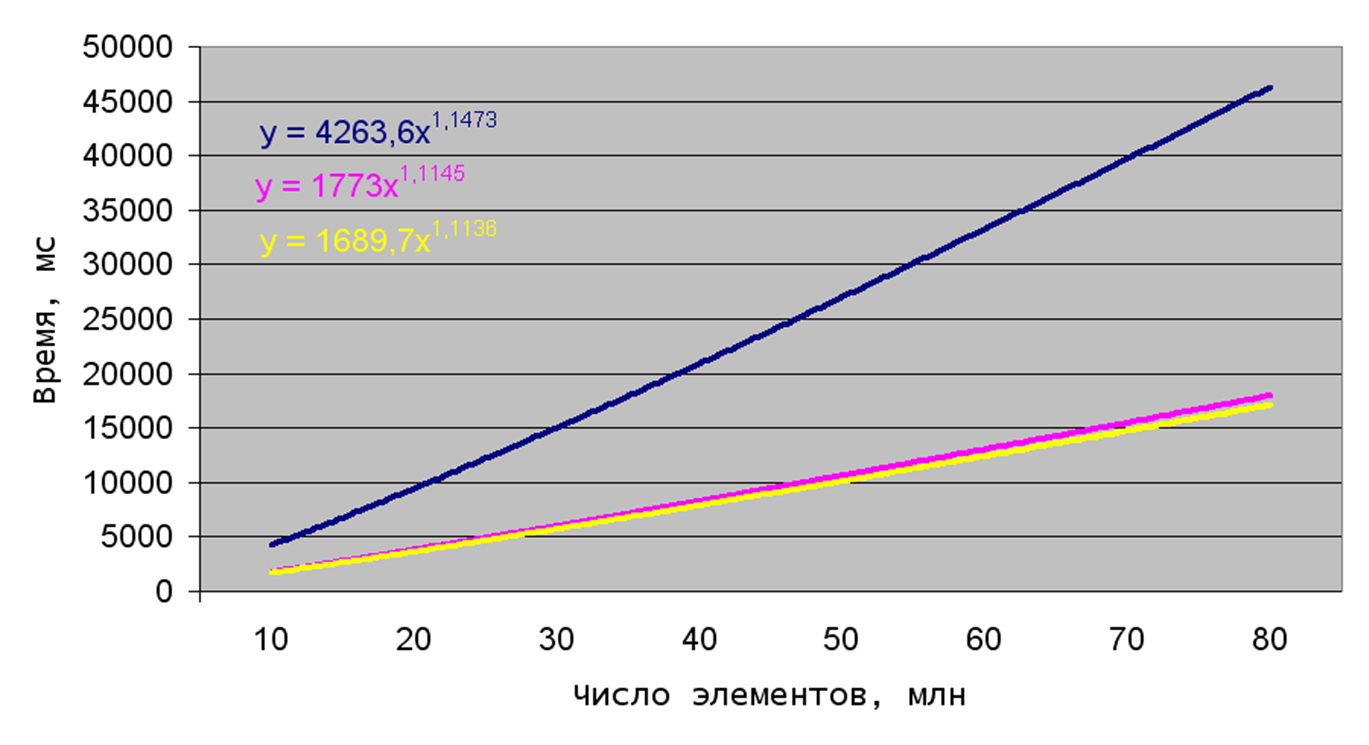
Рис. 1. Зависимость времени поразрядной сортировки от числа элементов
Здесь и далее синий цвет относится к случайному порядку входных данных, розовый – к обратно отсортированным данным и жёлтый – к уже отсортированным данным (см. рис. 1). Как видим, всё, казалось бы, неплохо, но, посмотрев на график времени сортировки слияниями, убеждаемся в обратном:
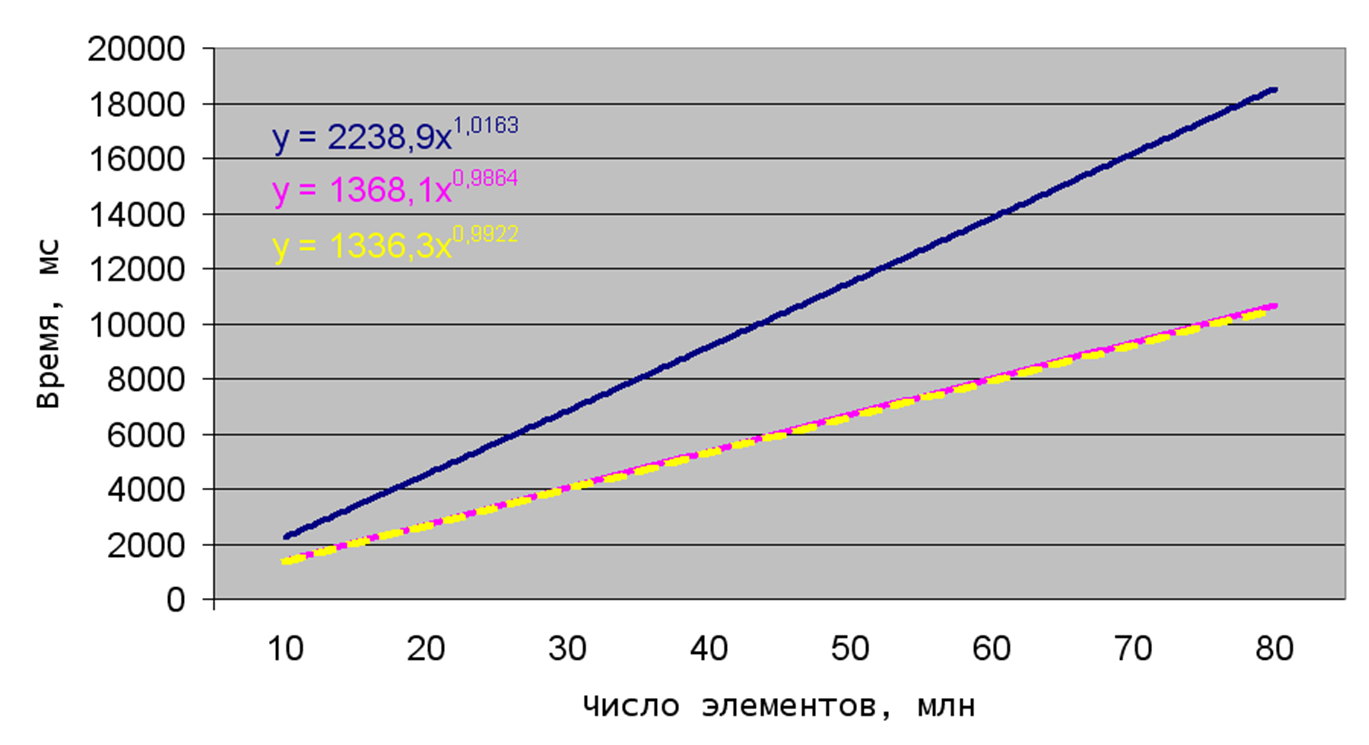
Рис. 2. Зависимость времени сортировки слияниями от числа элементов
Вот так вот... Будучи уверенным в идеальности поразрядной сортировки, я был неправ.
Теперь сортировка Шелла (рис. 3).
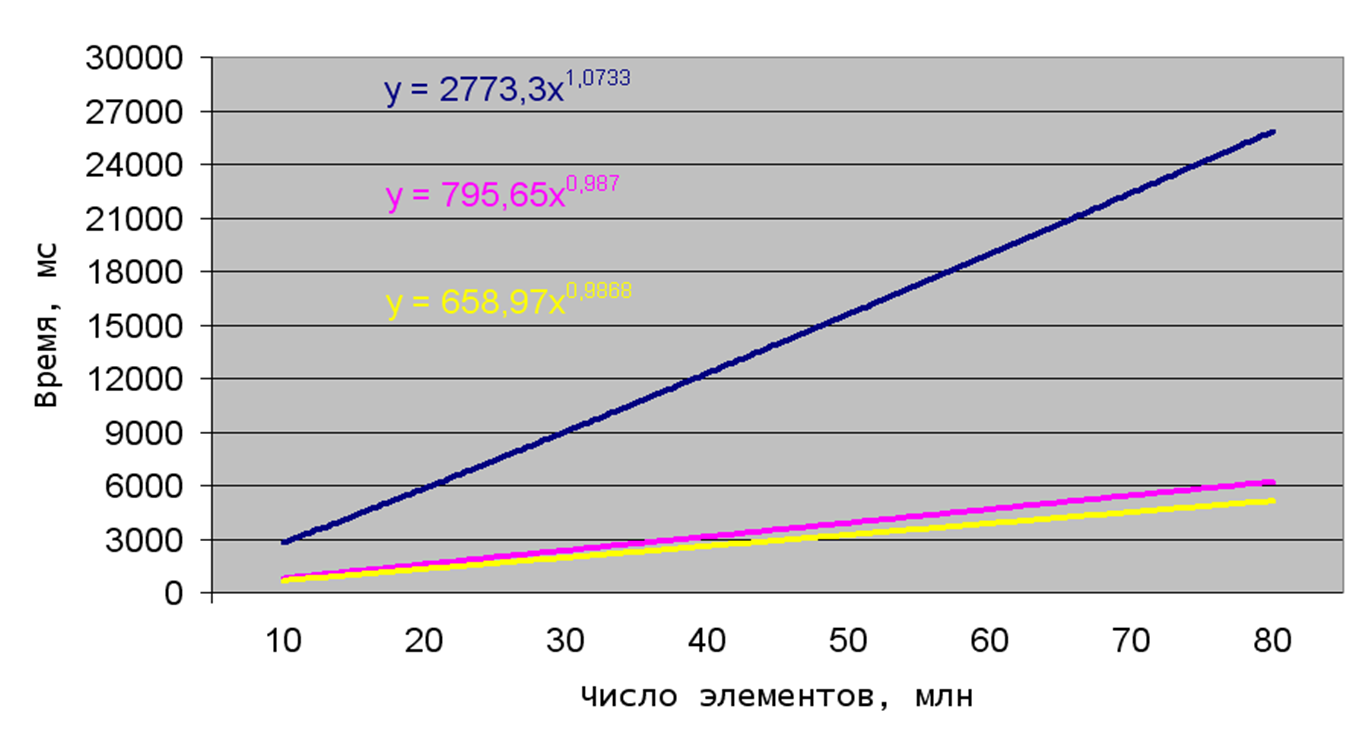
Рис. 3. Зависимость времени сортировки Шелла от числа элементов
Сортировка Шелла тоже, в принципе, неплоха, хотя и уступает сортировке слияниями в среднем. Но отсортированные в прямом и обратном порядке массивы для неё не представляют сложности, сортировка слияниями же несколько хуже.
А теперь о грустном. Теоретическая линейность поразрядной сортировки на практике оказалась нелинейнее нелинейности нелинейных сортировок слияниями и Шелла (такая вот тавтология). Почему так получилось я, честно признаться, не знаю. Есть предположение, что при генерации списка динамическая память выделяется в куче по соседним или близким адресам, и переход от элемента списка к следующему элементу не представляет особых сложностей – необходимо всего лишь добавить 12 (или даже 16 – менеджер оперативной памяти может оптимизировать процесс, выделяя память по хорошим адресам) к адресу данного элемента. Постепенно сортируя список разряд за разрядом, мы получаем всё более и более запутанное спагетти, и операция взятия адреса следующего элемента усложняется.
Кстати, родилась ещё одна мысль. Если менеджер памяти не умеет автоматически выравнивать данные по хорошим адресам, то именно это может приводить к замедлению. В любом случае я считаю, что применение поразрядной сортировки на практике для больших наборов данных нецелесообразно, почти 50 секунд на 80 миллионов элементов – неудовлетворительный результат!
Ещё одно предположение. Просматривая беглым взглядом тексты программ, представленных мной, можно заметить, что поразрядная сортировка пестрит выражениями в квадратных скобках! Обращения к памяти, по-видимому, значительно замедляют процесс, однако избежать их, увы, невозможно.
