Куб - Сфера

При рассмотрении вопроса об обратной трассировке лучей часто говорится, что один из самых простых и удобных для этого объектов - сфера. Это связано с лёгкостью определения точки пересечения (или определения её отсутствия) луча и сферы, а также с тем, что нормаль в точке касания совпадает по направлению с вектором, выпущенным из центра сферы к этой точке.

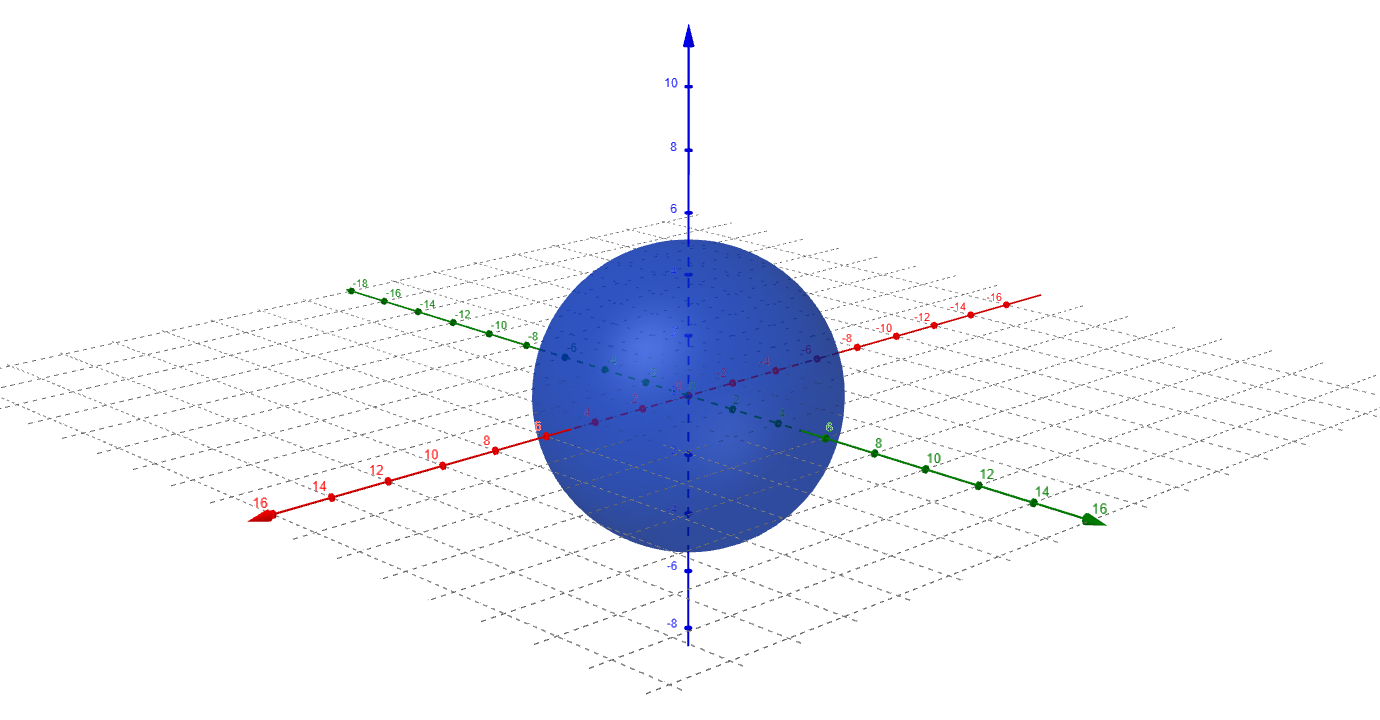
Один и тот же объект можно определить различными способами. Вспомним, какое множество точек соответствует сфере S с центром в точке $ O(x_0, y_0, z_0) $ радиуса $ r $ :

$$ S = \lbrace A(x, y, z) \in R^3 \ | \ \rho(O, A) = r \rbrace $$

Выбрав в качестве метрики функцию $ \rho(x, y) = \sqrt{(y_1 - x_1)^2 + (y_2 - x_2)^2 + (y_3 - x_3)^2} $, получим привычное нам уравнение сферы:

$$ (x - x_0)^2 + (y - y_0)^2 + (z - z_0)^2 = r^2 $$

Стоит отметить, что если в качестве $ \rho (x, y) $ брать другие функции (но всё же являющиеся метриками), то мы вновь будем получать сферы S, но в других метрических пространствах.

Заметим, что если мы выберем функцию $ \rho(x, y) $, как максимум из модулей разностей соответствующих координат:

$$ \rho(x, y) = \max(|y_1 - x_1|, |y_2 - x_2|, |y_3 - x_3|), $$

то получится, что мы задали куб с центром в точке $ O(x_0, y_0, z_0) $ и длиной стороны равной $ 2r $ . Причём, векторы нормалей к граням этого куба будут коллинеарны координатным осям.

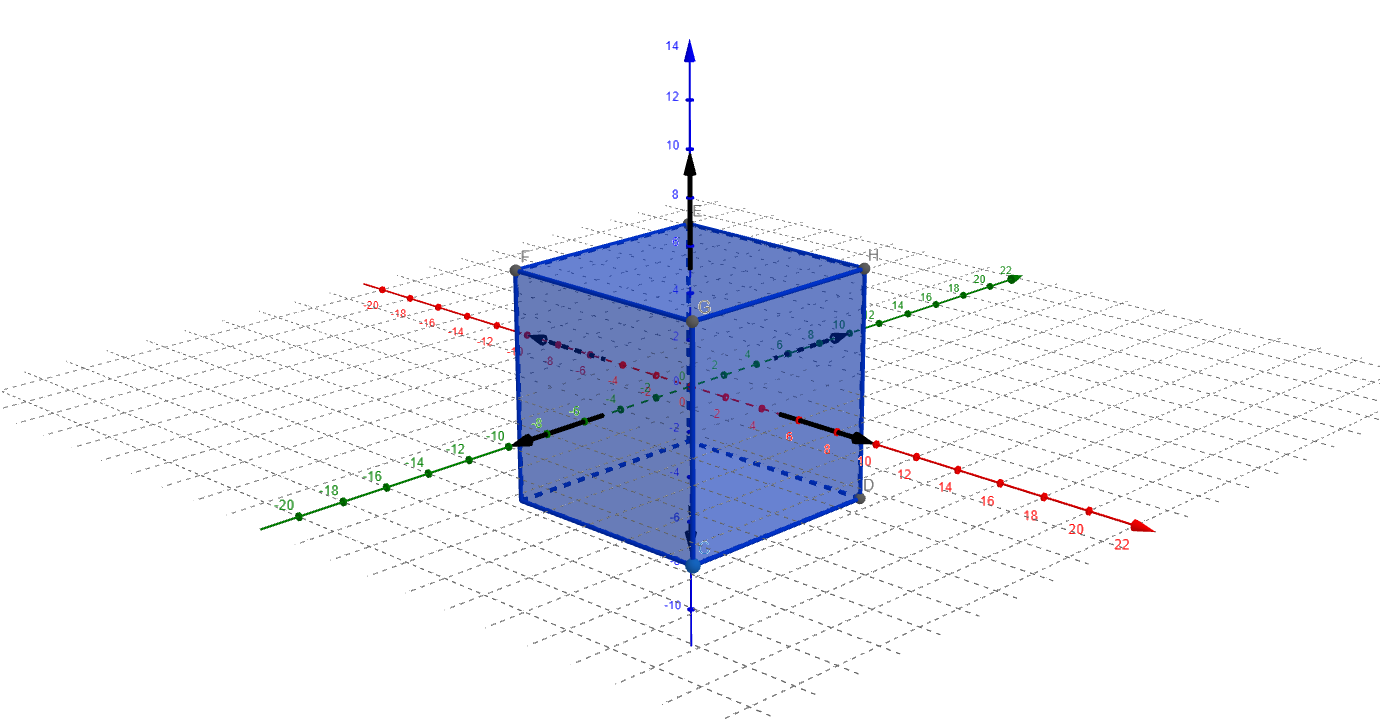
Получим для него и уравнение:

$$ \max(|x - x_0|, |y - y_0|, |z - z_0|) = r $$

Теперь будем искать точки пересечения луча и куба. Для этого подставим вместо $x, y, z$ соответствующие равенства из параметрической записи луча:

$$ \max(|x_s + \vec{\Delta}_x \cdot t - x_0|, |y_s + \vec{\Delta}_y \cdot t - y_0|, |z_s + \vec{\Delta}_z \cdot t - z_0|) = r $$

Таким образом, мы перешли к уравнению одной переменной $ t $. Его можно разбить на шесть линейных уравнений с ограничениями, пользуясь соображением:

$$ \max(x_1, x_2, ... , x_n) = a \Leftrightarrow (\exists k)(1 \leq k \leq n)((x_k = a) \& (\forall i \neq k)(x_i \leq x_k)) $$

Если приращение по какой-то координате нулевое, то соответствующие решения рассматривать не будем. Предположим, что $ \vec{\Delta}_x \neq 0, \vec{\Delta}_y \neq 0, \vec{\Delta}_z \neq 0 $, тогда сможем записать решения каждого уравнения:

$ t_1 = \frac{r + x_0 - x_s}{\vec{\Delta}_x} $	$ t_2 = -\frac{r + x_0 - x_s}{\vec{\Delta}_x} $
$ t_3 = \frac{r + y_0 - y_s}{\vec{\Delta}_y} $	$ t_4 = -\frac{r + y_0 - y_s}{\vec{\Delta}_y} $
$ t_5 = \frac{r + z_0 - z_s}{\vec{\Delta}_z} $	$ t_6 = -\frac{r + z_0 - z_s}{\vec{\Delta}_z} $

Сформируем из чисел $ t_1, t_2, ... , t_6 $ новый набор решений $ t_1', t_2', ... , t_s' $ так, чтобы для любого $ t_i' \ (1 \leq i \leq s \leq 6) $ выполнялась система неравенств:

$$ \begin{cases} |x_s + \vec{\Delta}_x \cdot t_i' - x_0| \leq r \\ |y_s + \vec{\Delta}_y \cdot t_i' - y_0| \leq r \\ |z_s + \vec{\Delta}_z \cdot t_i' - z_0| \leq r \end{cases} $$

Если набор решений $ t_1', t_2', ... , t_s' $ оказался не пуст, то параметру $ t = \min(t_1', t_2', ... , t_s') $ будет соответствовать точка пересечения луча и куба.

Замечание

Приведённое рассуждение справедливо только для куба с произвольным центром и гранями, нормали к которым коллинеарны координатным осям. Однако, мы можем воспользоваться соответствующим преобразованием пространства, чтобы свести общий случай (когда грани как-то повёрнуты относительно центра куба) к этому частному.

Вперёд

\( t_1 = \frac{r + x_0 - x_s}{\vec{\Delta}_x} \)	\( t_2 = -\frac{r + x_0 - x_s}{\vec{\Delta}_x} \)
\( t_3 = \frac{r + y_0 - y_s}{\vec{\Delta}_y} \)	\( t_4 = -\frac{r + y_0 - y_s}{\vec{\Delta}_y} \)
\( t_5 = \frac{r + z_0 - z_s}{\vec{\Delta}_z} \)	\( t_6 = -\frac{r + z_0 - z_s}{\vec{\Delta}_z} \)