Рассмотрим ещё один способ задания куба - пересечение шести плоскостей, каждая из которых описывается уравнением вида:

причём нормали к плоскостям должны смотреть "наружу". Это условие необходимо для корректного вычисления освещённости граней.

Следует отметить, что самый естественный для школьной геометрии способ задания куба - перечисление координат вершин, можно считать частным случаем обсуждаемого метода, так как по точкам вершин можно с лёгкостью составить уравнения плоскостей, а направление нормалей устанавливать согласно правилу правой руки.

Для каждой плоскости вычислим значение параметра \( t_i \), соответствующее точке пересечения плоскости и луча. Для каждого найденного решения \( t_1, t_2, ... , t_n \ (n \leq 6) \) нужно проверить, что точка лежит внутри пересечения всех полупространств, определяемых плоскостями куба, чтобы убедиться, что полученная точка действительно лежит на грани куба.

Такую проверку можно выполнять различными способами. Например, мы можем выполнять непосредственную подстановку координат полученной точки в уравнение плоскости. Также можно для каждой плоскости получать вектор нормали, проходящий через эту точку, а затем вычислять скалярное произведение исходной нормали и вычисленной и по его знаку определять принадлежность точки полупространству.

В обоих случаях для каждого решения придётся выполнить 6 (в случае оптимизации 4) проверок. Однако, можно обойтись и меньшим числом, если сохранять для куба его центр и половину длины стороны.

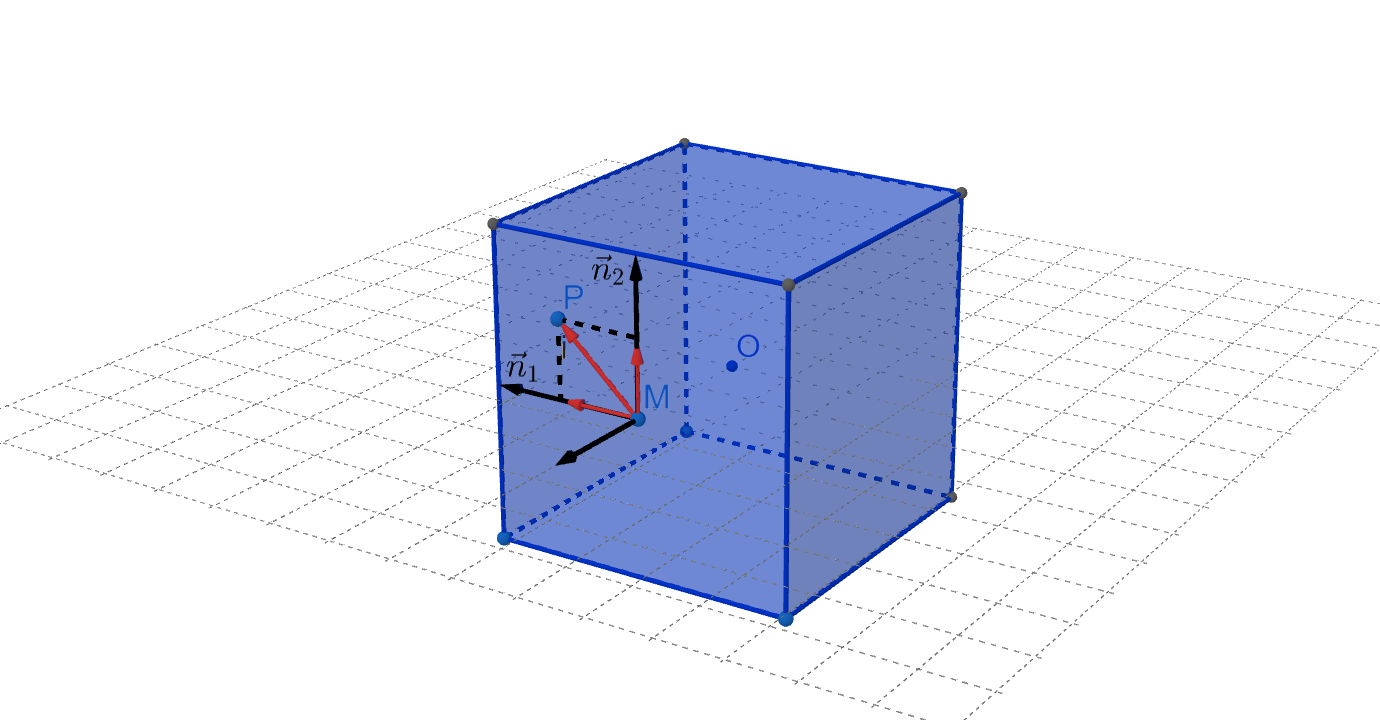
Когда мы получаем какое-то корректное значение параметра \( t \), то в этот момент точно знаем с какой гранью было зарегистрировано пересечение - точка \(P(x_p, y_p, z_p)\). Вычислим координаты точки \(M(x_m, y_m, z_m)\) путём прибавления к координатам центра куба вектора, равного нормали \( \vec{n} \) к этой грани (имеющей единичную длину), умноженной на \(r\):

Следует отметить, что для ускорения работы программы можно отдельно хранить и центры граней, вычислив их один раз при создании объекта.

Зададим вектор \( \overrightarrow{MP}(x_p - x_m, y_p - y_m, z_p - z_m) \) и спроецируем его на нормали к соседним граням \( \vec{n}_1, \vec{n}_2 \). Тогда мы можем сформулировать критерий: для того, чтобы точка \( P \) лежала на грани куба, необходимо и достаточно, чтобы длины проекций вектора, проведённого из центра грани к этой точке, на нормали соседних граней не превосходили \( r \).

Приняв за \( t \) наименьшее значение из всех \( t_i \), успешно прошедших проверку, получим значение параметра, при котором луч пересекает куб впервые.