Полезная информация

В этом разделе будет собрана информация, с которой необходимо ознакомиться для более полного понимания рассуждений и обоснований на других страницах сайта.

Луч наблюдателя

Картинка: wikimedia

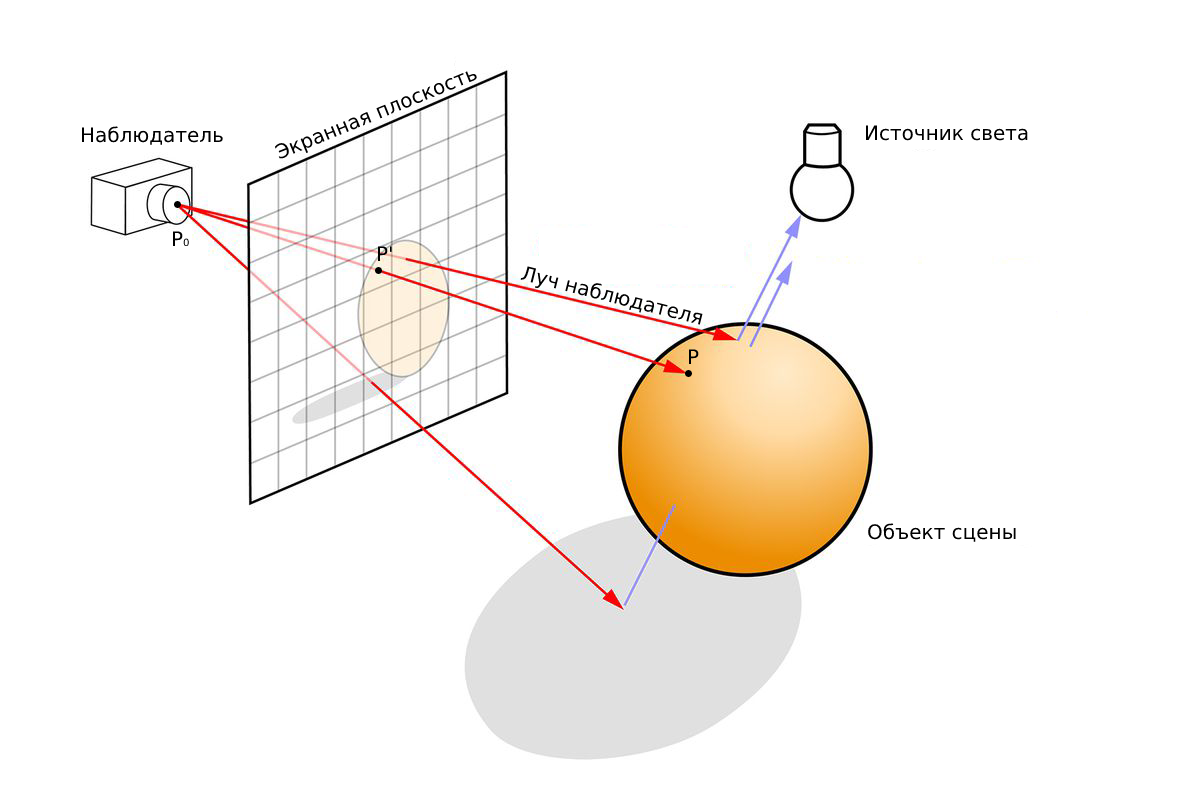
Выпустим луч, проходящий через точку наблюдателя $p_0(x_s, y_s, z_s)$ ( $ s $ - spectator) и середину пикселя $p'(x', y', z')$ экранной плоскости. Тогда координаты произвольной точки $p(x, y, z)$, лежащей на этом луче можно вычислить по формуле:

$$ p = p_0 + (p' - p_0)t, \qquad t > 0 $$

Зададим вектор $ \vec{\Delta} = p' - p_0$ и запишем равносильное тождество в виде системы для каждой координаты точки $p(x, y, z)$:

$$ \begin{cases} x = x_s + \vec{\Delta}_x \cdot t \\ y = y_s + \vec{\Delta}_y \cdot t \\ z = z_s + \vec{\Delta}_z \cdot t \end{cases} $$

Преобразование пространства

Будем задавать куб, произвольно расположенный в пространстве, задав координаты его центра, половину длины стороны, и углов поворота нормалей, сонаправленных с координатными осями, вокруг них.

Наша задача - получить такую матрицу преобразования, чтобы после её воздействия центр куба совместился с началом координат, а векторы нормалей к граням стали коллинеарны координатным осям.

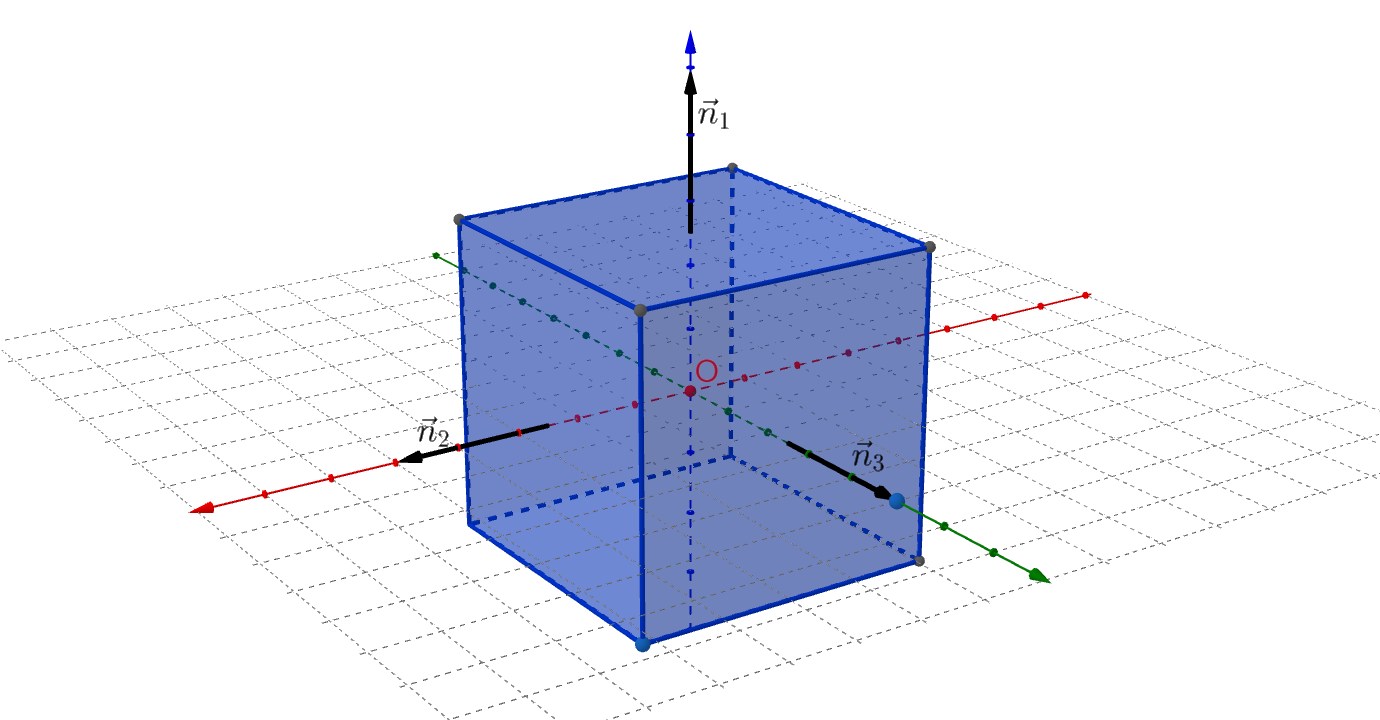
Следует отметить, что ориентация куба в пространстве однозначно определяется его центром и углами поворота нормалей, причём достаточно задать только три попарно ортогональных вектора, поэтому в дальнейшем мы будем говорить именно о повороте нормалей.

Пусть углы поворота нормалей вокруг осей $Ox, Oy, Oz$ равны $\alpha, \beta, \gamma$ соответственно. Выведем матрицу преобразования к частному случаю расположения куба - $ M_1 $. Для этого переместим центр куба в начало координат, а затем будем поворачивать его нормали на углы $-\alpha, -\beta, -\gamma$ вокург осей $Ox, Oy, Oz$ соответственно. Тогда можно записать матрицу $ M_1 $ в следующем виде:

$$ M_1 = T \cdot R_x \cdot R_y \cdot R_z $$

$$ M_1 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ -x_0 & -y_0 & -z_0 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos(-\alpha) & \sin(-\alpha) \\ 0 & -\sin(-\alpha) & \cos(-\alpha) \\ 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} \cos(-\beta) & 0 & -\sin(-\beta) \\ 0 & 1 & 0 \\ \sin(-\beta) & 0 & \cos(-\beta) \\ 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} \cos(-\gamma) & \sin(-\gamma) & 0 \\ -\sin(-\gamma) & \cos(-\gamma) & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix} $$

Отметим, что мы работаем с однородными координатами, поэтому не будем явно прописывать последний (состоящий из нулей и одной единицы на главной диагонали) столбец в матрицах при записи формул.

Аналогичным образом получим и матрицу для обратного преобразования $M_2$, которая понадобится для преобразования нормалей к граням:

$$ M_2 = \begin{pmatrix} \cos(\gamma) & \sin(\gamma) & 0 \\ -\sin(\gamma) & \cos(\gamma) & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} \cos(\beta) & 0 & -\sin(\beta) \\ 0 & 1 & 0 \\ \sin(\beta) & 0 & \cos(\beta) \\ 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0\\ 0 & \cos(\alpha) & \sin(\alpha) \\ 0 & -\sin(\alpha) & \cos(\alpha) \\ 0 & 0 & 0 \\ \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ x_0 & y_0 & z_0 \\ \end{pmatrix} $$

Теперь, для получения точки пересечения луча $ p $ и куба, нужно сделать следующее:

с помощью матрицы $ M_1 $ изменить начальную точку луча $ p_0 $ и вектор приращений $ \vec{\Delta} $
в новых координатах решить задачу о нахождении значения параметра $ t' $, соответствующего точке пересечения в частном случае. Примечательно, что значение параметра $ t' $ будет равно значению параметра $ t $ в точке пересечения для исходных координат.

Таким образом, по значению параметра $ t $ мы можем однозначно установить точку пересечения (если она есть) луча и куба для его произвольного расположения.

Вперёд