Удивительные числа

Если предмет не имеет правильного облика, он не работает.
Леонардо да Винчи.

Что же такое последовательность? Это набор элементов некоторого множества. Каждый элемент в котором последовательно выбран по какому-нибудь его свойству или по особой связи другими элементами. Вот об этих свойствах и взаимосвязях мы здесь и поговорим.

Профессор ВГПУ В.С. Губа однажды сказал, что практически под любую последовательность можно "подвести" какую-либо "закономерность". Вопрос может быть лишь в том, насколько прост будет закон описания. Если есть что-то, с чем другие версии явно не конкурируют, то ясно, какой ответ является "правильным".

Начнем с чего-нибудь простого. И попробуем разобраться - что же будет дальше.

Возьмем, например, такую последовательность:
1 2 4 ?

Какое число стоит дальше? 8? Да, то есть каждый предыдущий в 2 раза больше следующего. А может 7? Тоже верно. Если смотреть разницу между соседними элементами. 2-1=1, 4-2=2, ?-4=3! Откуда и получаем нашу 7. Как говорилось выше, что почти любую последовательность можно "подвести" под какую-либо "закономерность", нам удалось это сделать и выявить 2 закономерности, но, я думаю, можно найти и больше.

О любых последовательностях, которых тут не представлено, можно почитать на сайте.

Рассмотрим последовательность простых чисел, которая до сих пор остается не такой простой:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97...
попробуйте, может у вас получиться постичь порядок и закономерности их расположения, может быть именно вы разгадаете их тайну? Алгоритм, который ищет эти числа назавается "Решето Эратосфена", он берет все числа и отсеивает составные, при этом остаются только простые. То есть сначала выписываем все числа от 2 до заданного N. Затем берем 2 - это простое число, обводим в круг, потом вычеркиваем все числа с шагом 2 (то есть четные). Потом берем следующее не вычеркнутое за двойкой число - это 3 - обводим в круг, снова вычеркиваем с шагом 3, замечу, что 6 уже была вычеркнута, как кратная 2. Следующее не вычеркнутое за тройкой - это 5 - тоже обводим в круг. Вычеркиваем кратные 5.....и так далее. Те цифры, которые обведены, и являются простыми.

В последовательности простых чисел также ищут некоторые подмножества и уже в них рассматривают закономерности, пытаясь хоть как-то решить их загадку.

Возможно, вам встречались простые-близнецы. Что это? Это пара простых чисел, у которых модуль разности между ними равен 2. Для наглядности приведу несколько первых пар:
(3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103)...

Также большой интерес вызывают  простые палиндромы. Например,
2, 3, 5, 7, 11, 101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757...

А зачем же вообще нужны простые числа? Они служат "базисом" составных чисел. Основная теорема арифметики гласит, что каждое натуральное число (которое больше 1) представимо в виде произведения простых чисел, причём единственным способом. То есть они составляют составные.

Среди простых чисел особый интерес также вызывают простые числа Мерсенна - числа вида М_р = 2^p - 1, где p - простое число. Названы они в честь французского монаха Мерена Мерсенна - одного из основателей Парижской Академии наук.

Очевидно, что для индексов p = 2, 3, 5, 7 результат получается простым, но для p = 11 получается составным: М₁₁= 2047 = 23*89. Вот опять математики придумали себе занятие - найти самое большое простое число.

Конечно, что все числа Мерсена невозможно рассмотреть, но это пытаются сделать. Например, в 2009 году за нахождение 45-го простого числа Мерсенна М_43112609 (десятичная запись которого содержит не менее 10 миллионов цифр)  была получена премия в 100 000 $, назначенная сообществом Electronic Frontier Foundation. А на данный момент самое большое простое число М_57885161, которое  содержит 17425170 десятичных цифр.

Почему же к числам Мерсена вызван такой интерес? Из-за связи с совершенными числами. А в совершенных числах много не только интересного, но и, в какой-то мере, загадочного. До сих пор не нашли ответ на вопрос - конечно ли множество совершенных чисел или бесконечно, есть ли среди совершенных чисел нечетные? Леонард Эйлер доказал, что все четные совершенные числа имеют вид 2^p-1*М_р, где М_р - простое число Мерсенна. Но описал ли он этой формулой все совершенные числа?

Рассмотрим еще одну последовательность, может быть вы, мой читатель, уже встречались с ней в задачах по комбинаторике, так как она очень часто там встречается. Это числа Каталана, названы в честь бельгийского математика.

Вот первые несколько чисел последовательности:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012...

Сами числа выражаются формулой , где "!" - факториал.

Википедия утверждает, что известно, как минимум 66 различных конструкций, которые описывают числа Каталана. Рассмотрим некоторые из них:

• C_n подсчитывает количество выражений, содержащих n пар скобок, которые правильно написаны, например:
  ((())) () (()) () () () (()) () (() ())

• Двоичные деревья – деревья, из каждого узла которых (кроме листьев) выходит ровно две ветки. И опять число Каталана - количество бинарных деревьев с заданным числом листьев.
  
• Монотонные пути в сетке – маршруты из левого нижнего угла квадрата в правый верхний, которые не проходят выше диагонали.
  
• Количество различных способов разрезать прямыми линиями выпуклый многоугольник на треугольники.
  

Так мы с помощью примеров и узнали о применении.

Ну и напоследок я расскажу, по моему мнению, про самую интересную последовательность. Она встречается в самых неожиданных местах.

Как вы думаете, что общего между отпечатками пальцев, подсолнухом, ухом человека, продуктами Apple, раковиной моллюсков, дизайном....этот список можно продолжать бесконечно. Именно этой последовательности посвящен эпиграф к этой странице. Да, все эти вещи стремятся быть идеальными.

"Какой же критерий у идеальности?" - спросите вы. Давайте посмотрим на интерфейс всеми известной социальной сети - Twitter :

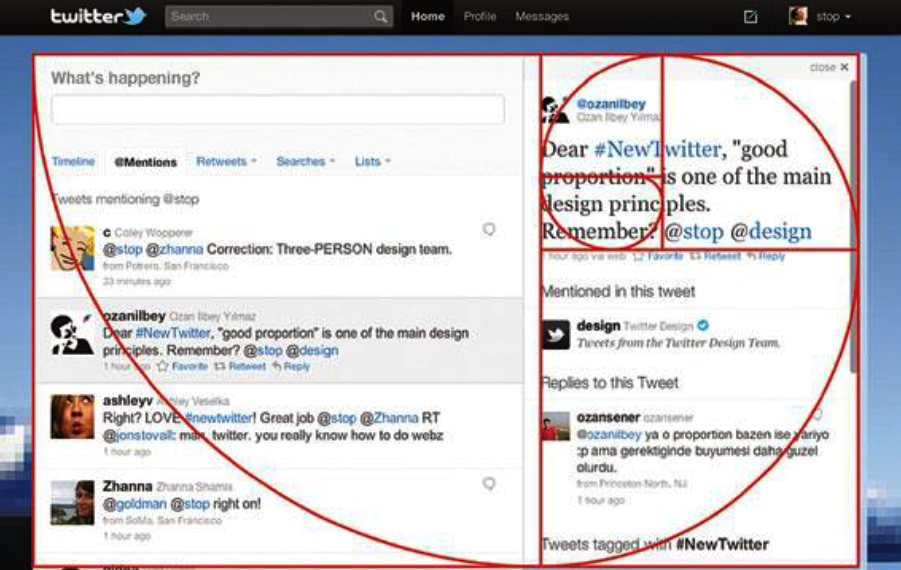
Из геометрических соображений он идеален - у него идеальные пропорции. Twitter имеет удобную разметку страницы, которая является привлекательной для человеческого глаза. Причина тому - золотое сечение - cпираль, которая выделена красным. Очень часто дизайнеры пользуются этим принципом, потому что подсознание сразу замечает идеальные пропорции, и их продукт становится заметным среди других.

Какое отношение она имеет к нашей последовательности? Для ответа на этот вопрос рассмотрим прямоугольник. Нет, не просто прямоугольник, а идеальный, золотой.

 

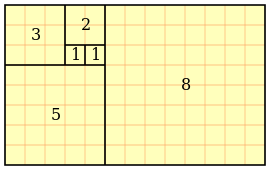
Рассмотрим длины сторон по возрастанию: 1, 1, 2, 3, 5, 8, 13.

Да, это числа Фибоначчи. Даже спирали галактик подчиняются этой последовательности.

Про нее можно говорить много, но, надеюсь, я вас заинтересовала и вы будете уже самостоятельно изучать дальше бесконечный и удивительный мир...

 

наверх | дальше